Displacement thickness : The effect of viscosity in the boundary layer is to retard the flow. So, the mass flow rate adjacent to the solid surface is less than the mass flow rate that would pass through the same region in the absence of boundary layer. In the absence of viscous forces, the velocity in the vicinity of sold surface would be Uas shown in Fig. 5.7.3(b). 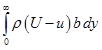The decrease in the mass flow rate due to the influence of viscous forces is , where b is the width of the surface in the direction perpendicular to the flow. So, the displacement thickness is the distance by which the solid boundary would displace in a frictionless flow (Fig. 5.7.3-b) to give rise to same mass flow rate deficit as exists in the boundary layer (Fig. 5.7.3-c). The mass flow rate deficiency by displacing the solid boundary by will be . In an incompressible flow, equating these two terms, the expression for is obtained.

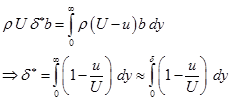(5.7.1)

Momentum thickness : The flow retardation in the boundary layer also results the reduction in momentum flux as compared to the inviscid flow. The momentum thickness is defined as the thickness of a layer of fluid with velocity U, for which the momentum flux is equal to the deficit of momentum flux through the boundary layer. So, the expression for in an incompressible flow can be written as follow;

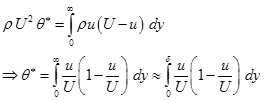(5.7.2)

The displacement/momentum thickness has the following physical implications;

• •  The displacement thickness represents the amount of distance that thickness of the body must be increased so that the fictitious uniform inviscid flow has the same mass flow rate properties as the actual flow.

•  It indicates the outward displacement of the streamlines caused by the viscous effects on the plate.

•  The flow conditions in the boundary layer can be simulated by adding the displacement thickness to the actual wall thickness and thus treating the flow over a thickened body as in the case of inviscid flow.

•  Both are the integral thicknesses and the integrant vanishes in the free stream. So, it is relatively easier to evaluate as compared to .

The boundary layer concept is based on the fact that the boundary layer is thin. For a flat plate, the flow at any location x along the plate, the boundary layer relations are true except for the leading edge. The velocity profile merges into the local free stream velocity asymptotically. The pressure variation across the boundary layer is negligible i.e. same free stream pressure is impressed on the boundary layer. Considering these aspects, an approximate analysis can be made with the following assumptions within the boundary layer.

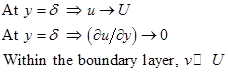(5.7.3)