Laminar Flow Solutions
The exact solution of Navier-Stokes equation for the steady, incompressible, laminar flow through a circular pipe of constant cross-section is commonly known as Hagen-Poiseuille flow. Specifically, for laminar flow, the expression for shear stress (Eq. 5.4.13) can be represented in the following form;
 |
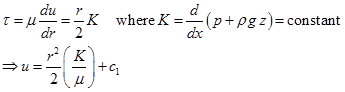(5.4.15) |
Eq. (5.4.15) can be integrated and the constant of integration is evaluated from no-slip condition, i.e. 
. After substituting the value of 
, Eq. (5.4.15) can be simplified to obtain the laminar velocity profile for the flow through circular pipe which is commonly known as Hagen-Poiseuille flow. It resembles the nature of a paraboloid falling zero at the wall and maximum at the central line (Fig. 5.4.1 and Eq. 5.4.16).
 |
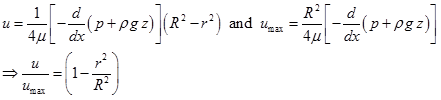(5.4.16) |
The simplified form of velocity profile equation can be represented as below;
 |
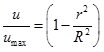(5.4.17) |
Many a times, the pipe is horizontal so that 
and the other results such as volume flow rate 
and average velocity 
can easily be computed.
 |
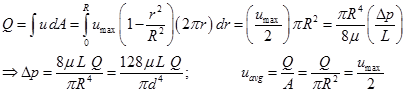(5.4.18) |
The wall shear stress is obtained by evaluating the differential (Eq. 5.4.15) at the wall 
which is same as of Eq. (5.4.14)
 |
(5.4.19) |
Referring to Eq. (5.4.6), the laminar friction factor can be calculated as,
 |
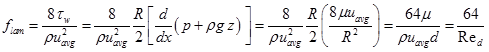(5.4.20) |
The laminar head loss is then obtained from Eq. (5.4.7) as below;
 |
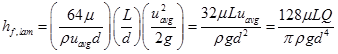(5.4.21) |
The following important inferences may be drawn from the above analysis;
- The nature of velocity profile in a laminar pipe flow is paraboloid with zero at the wall and maximum at the central-line.
- The maximum velocity in a laminar pipe flow is twice that of average velocity.
- In a laminar pipe flow, the friction factor drops with increase in flow Reynolds number.
- The shear stress varies linearly from center-line to the wall, being maximum at the wall and zero at the central-line. This is true for both laminar as well as turbulent flow.
- The wall shear stress is directly proportional to the maximum velocity and independent of density because the fluid acceleration is zero.
- For a certain fluid with given flow rate, the laminar head loss in a pipe flow is directly proportional to the length of the pipe and inversely proportional to the fourth power of pipe diameter.