It is to be noted that does not vary with θ and at the inner and outer radii, there is no velocity. So, the motion can be treated as purely circumferential so that . The θ -momentum equation may be written as follows;

(5.3.6)

Considering the nature of the present problem, most of the terms in Eq. (5.3.6) will vanish except for the last term. Finally, the basic equation for the flow between rotating cylinders becomes a linear second-order ordinary differential equation.

(5.3.7)

The constants appearing in the solution of are found by no-slip conditions at the inner and outer cylinders;

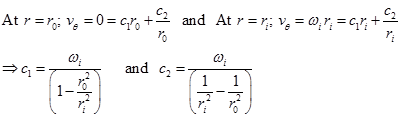(5.3.8)

The final solution for velocity distribution is given by,

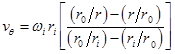(5.3.9)