This equation can be differentiated with respect t to obtain the net force acting on the fluid mass.

(2.1.7)

Here, is the net external force acting on i^th particle.

The other way to represent the same law is in terms of angular momentum and for a fluid mass, it is expressed as,

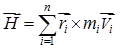(2.1.8)

where, is the position vector of the particle with respect to certain frame of reference.

The rate of change of angular momentum is given by,

(2.1.9)

Here, is the net external momentum acting on the fluid mass. In other words, the rate of change of angular momentum of a system of fluid particle is equal to the net external moment on the system.

First law of thermodynamics : This law is nothing but the energy conservation law which states that energy can neither be created nor be destroyed but, can be changed from one form to another. If is the heat exchange with the system, is the work done by the system and dE is the change in energy of the system, then they are related by the following expressions for a closed system.

(2.1.10)

Second law of thermodynamics : This law introduces a new property i.e. entropy (S) and the change in the entropy (dS) is related to the heat transfer and the absolute temperature (T).

(2.1.11)

This inequality accounts for flow analysis involving losses due to friction, viscous dissipation and any other means of non recoverable losses. Minimizing the loss in available energy in any flow situation is of obvious fact of engineering importance.