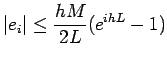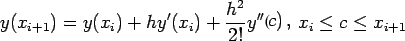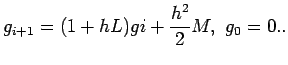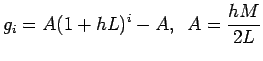Next: 3. Runge-Kutta Method
Up: 2. Error Estimates and
Previous: 2. Error Estimates and
Let
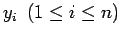 be the approximations of a
solution y of (2.1) at
be the approximations of a
solution y of (2.1) at 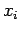 .Let the (exact)solution y be twice
continually differentiable on [a,b],
.Let the (exact)solution y be twice
continually differentiable on [a,b],
 . Further let
. Further let
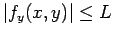
and
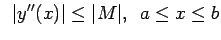
where L and M are positive constants. Then
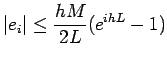 |
(2.3) |
Proof:
By the mean value we have,
we also know,
Substraction, now leads to,
 |
(2.4) |
Again, by mean value theorem
where d lies between 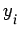 and
and 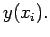 Substituting in (2.4)we
get
Substituting in (2.4)we
get
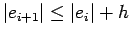 L L |
(2.5) |
Let 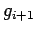 be the solution of the difference equation
be the solution of the difference equation
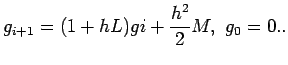 |
(2.6) |
Claim:
The claim follows by induction. Also by induction
The theorem now is proved once we notice
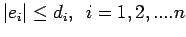
Remark: Inequality (2.3) implies that the error is 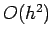 .
Theorem also given an upper band for the error.
.
Theorem also given an upper band for the error.



Next: 3. Runge-Kutta Method
Up: 2. Error Estimates and
Previous: 2. Error Estimates and
root
2006-02-16