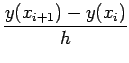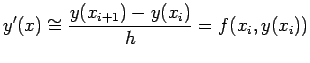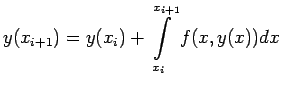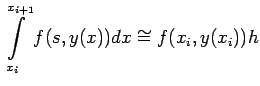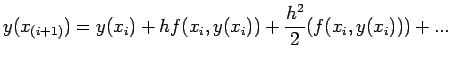Next: 1.3 Example:
Up: 1
Previous: 1.1
Consider the problem (1.1.1). Let
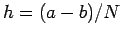 be the step size. Let
be the step size. Let
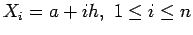 , with
, with 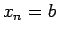 .
Let
.
Let 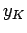 be the approximate value of y at
be the approximate value of y at 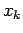 . We define
. We define
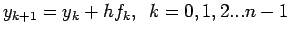 |
(1.2.1) |
where
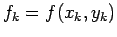 . The method of determination of
. The method of determination of 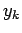 by (1.2.1) is
called the Euler's method.
by (1.2.1) is
called the Euler's method.
Remark : Euler's method is an one-step method. The Euler's
method has many motivation. Firstly the derivative y' at 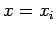 can be
approximated by
if h is sufficiently small. With this approximation in (1.1.1)
we have
we can also look at (1.2.1) from the following point of View.
Integration of (1.1.1) yields
can be
approximated by
if h is sufficiently small. With this approximation in (1.1.1)
we have
we can also look at (1.2.1) from the following point of View.
Integration of (1.1.1) yields
The integral on the right hand side now is approximated by
for sufficiently small 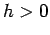 .
.
Secondly if y is differentiable sufficient number of times, we use
Taylor's expansion
neglecting terms containing with powers of 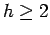 , we arrive
at (1.2.1). We illustrate the Euler's Algorithm with an example.
, we arrive
at (1.2.1). We illustrate the Euler's Algorithm with an example.
root
2006-02-16