
Next:Algorithm (Runge-Kutta) method of order 4 : Main Previous: 3.3 Algorithm (Runge-Kutta) methodExample
Find the approximate value of the solution IVP
with the step size (1) 0.1 (2) 0.05 and (3) 0.025 by using Runge-Kutta method of order 2. Calculate the error and tabulate the results.
Solution: Comparing the given IVP with (1.) we note that,a = 0, b = 0.5 and
.Calculate
and
from R-K method order 2 and use the formula
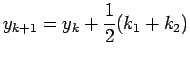
(usual notations are used ). The results are shown in Tables 4, 5 and 6.
Runge - Kutta Method of order 2
| Table 4 | |||||||
| Initial x | Initial y | Stepsize h | Appx. Y | Exa. Y | Error | k1 | k2 |
| 0.00000 | 1.00000 | 0.10000 | 1.00000 | 1.00000 | 0.00000 | 0.1 | 0.121 |
| 0.1000000 | 1.00000 | 0.10000 | 1.1105 | 1.11111 | 0.00061 | 0.1 | 0.146531 |
| 0.2000000 | 1.11050 | 0.10000 | 1.233765513 | 1.25000 | 0.01623 | 0.123321 | 0.184168 |
| 0.3000000 | 1.23377 | 0.10000 | 1.387510219 | 1.42857 | 0.04106 | 0.152218 | 0.237076 |
| 0.4000000 | 1.38751 | 0.10000 | 1.582157194 | 1.66667 | 0.08451 | 0.192518 | 0.314947 |
| 0.5000000 | 1.58216 | 0.1000000 | 1.835890108 | 2.00000 | 0.16411 | 0.250322 | 0.006266 |
| Table 5 | |||||||
| Initial x | Initial y | Stepsize h | Appx. Y | Exa. Y | Error | k1 | k2 |
| 0 | 1 | 0.05 | 1 | 1 | 0 | 0.05 | 0.055125 |
| 0.05 | 1 | 0.05 | 1.0525625 | 1.052631579 | -6.9079E-05 | 0.055394 | 0.061378 |
| 0.1 | 1.0525625 | 0.05 | 1.110948907 | 1.111111111 | -0.0001622 | 0.06171 | 0.068756 |
| 0.15 | 1.110948907 | 0.05 | 1.176182339 | 1.176470588 | -0.00028825 | 0.06917 | 0.077545 |
| 0.2 | 1.176182339 | 0.05 | 1.249540038 | 1.25 | -0.00045996 | 0.078068 | 0.088127 |
| 0.25 | 1.249540038 | 0.05 | 1.332637341 | 1.333333333 | -0.00069599 | 0.088796 | 0.101024 |
| 0.3 | 1.332637341 | 0.05 | 1.427547224 | 1.428571429 | -0.0010242 | 0.101895 | 0.11696 |
| 0.35 | 1.427547224 | 0.05 | 1.536974305 | 1.538461538 | -0.00148723 | 0.118115 | 0.136966 |
| 0.4 | 1.536974305 | 0.05 | 1.664514529 | 1.666666667 | -0.00215214 | 0.13853 | 0.162549 |
| 0.45 | 1.664514529 | 0.05 | 1.815054023 | 1.818181818 | -0.0031278 | 0.164721 | 0.195975 |
| 0.5 | 1.815054023 | 0.05 | 1.995402285 | 2 | -0.00459772 | 0.199082 | 0.240788 |
| Table 6 | |||||||
| Initial x | Initial y | Stepsize h | Appx. Y | Exa. Y | Error | k1 | k2 |
| 0 | 1 | 0.025 | 1 | 1 | 0 | 0.025 | 0.026266 |
| 0.025 | 1 | 0.025 | 1.025625 | 1.025641026 | -1.6026E-05 | 0.026298 | 0.027664 |
| 0.05 | 1.025625 | 0.025 | 1.051923467 | 1.052631579 | -0.00070811 | 0.027664 | 0.029138 |
| 0.075 | 1.051923467 | 0.025 | 1.078930846 | 1.081081081 | -0.00215023 | 0.029102 | 0.030693 |
| 0.1 | 1.078930846 | 0.025 | 1.106685431 | 1.111111111 | -0.00442568 | 0.030619 | 0.032337 |
| 0.125 | 1.106685431 | 0.025 | 1.135228679 | 1.142857143 | -0.00762846 | 0.032219 | 0.034073 |
| 0.15 | 1.135228679 | 0.025 | 1.164605572 | 1.176470588 | -0.01186502 | 0.033908 | 0.035911 |
| 0.175 | 1.164605572 | 0.025 | 1.194865028 | 1.212121212 | -0.01725618 | 0.035693 | 0.037857 |
| 0.2 | 1.194865028 | 0.025 | 1.226060373 | 1.25 | -0.02393963 | 0.037581 | 0.03992 |
| 0.225 | 1.226060373 | 0.025 | 1.258249888 | 1.290322581 | -0.03207269 | 0.03958 | 0.042109 |
| 0.25 | 1.258249888 | 0.025 | 1.291497448 | 1.333333333 | -0.04183589 | 0.041699 | 0.044435 |
| 0.275 | 1.291497448 | 0.025 | 1.32587326 | 1.379310345 | -0.05343709 | 0.043948 | 0.04691 |
| 0.3 | 1.32587326 | 0.025 | 1.361454731 | 1.428571429 | -0.0671167 | 0.046339 | 0.049547 |
| 0.325 | 1.361454731 | 0.025 | 1.398327491 | 1.481481481 | -0.08315399 | 0.048883 | 0.05236 |
| 0.35 | 1.398327491 | 0.025 | 1.436586603 | 1.538461538 | -0.10187494 | 0.051595 | 0.055367 |
| 0.375 | 1.436586603 | 0.025 | 1.476338004 | 1.6 | -0.123662 | 0.054489 | 0.058586 |
| 0.4 | 1.476338004 | 0.025 | 1.517700238 | 1.666666667 | -0.14896643 | 0.057585 | 0.062038 |
| 0.425 | 1.517700238 | 0.025 | 1.560806538 | 1.739130435 | -0.1783239 | 0.060903 | 0.065749 |
| 0.45 | 1.560806538 | 0.025 | 1.605807372 | 1.818181818 | -0.21237445 | 0.064465 | 0.069745 |
| 0.475 | 1.605807372 | 0.025 | 1.652873554 | 1.904761905 | -0.25188835 | 0.0683 | 0.074061 |
| 0.5 | 1.652873554 | 0.025 | 1.702200096 | 2 | -0.2977999 | 0.072437 | 0.078733 |
Remark. The local error in the Algorithm 3.3 is
. To achieve this error, we are forced to do more computation or in other words spend time to compute
and
. It all depends on the nature of the function to estimate the time consumed for the computation. The cost we pay for higher accuracy is more computation. Also, to reduce the local error, we need smaller values of the step size h, which again results in large number of computation. Each computation leads to more of rounding errors. In other words, reduction in discretization error may lead to increase in rounding off error. The moral is that the indiscriminate reduction of step-size need not mean more accuracy.