Next: 2.1 Theorem: Up: Main Previous: 1.2 Example:

2.Error Estimates and convergence

When we develop a method, specially to get approximate values of a certain quantity , it is desirable to know how much of deviation we have made from the original or created value. This difference of the exact and the computed value is usually known as the error comitted. An estimate for this error also indicates how good the calculated approximate value is. Such a feature may not be be possible , in general. Euler's method, is one such method which allows us for an analysis of the error, which is the main aim of this section.

Recall that
a).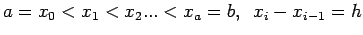 $a=x_0 < x_1 < x_2 ... < x_a =b , \,\, \, x_i - x_{i-1}=h$
b). is the approximate solution of the initial value problem

defined by the Euler's method namely

$$y_i = y_{i-1}+f(x_i,y_{i-1}),\,\,\, 1\leq i \leq n$$ (2..2)

Note here is the approximate value of $y(x_i)\,\,(1\leq i \leq n)$.The quantity $e_i$, defined by

$$e_i = y(x_i)-y_i,\,\,\, (1\leq i \leq n)$$

is therefore the deviation of from $y(x_i)$ or the error committed at the $i^{th}$ step. It is also called the truncation or discretization error. In this section, we examine the nature of $e_i$. It is desirable that $e_i$ is "small" when the step size h is small. In this connection we have the following result.

Next: 2.1 Theorem:Up:Main Previous: 1.2 Example: