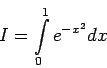Exercise

1. Show that
   $\Delta^r f_k = \nabla ^r f_{k+r}= \delta ^r f_{k+ \frac{r}{2}}$
   $\nabla^r f_k = \Delta ^r f_{k-r}= \delta ^r f_{k- \frac{r}{2}}$
   $\delta^rf_k=\Delta^rf_{k- \frac{r}{2}}=\nabla^rf_{k+\frac{r}{2}}$
   $\Delta\nabla f_k=\nabla\Delta f_k=\delta^2f_k$
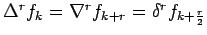
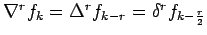
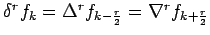
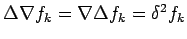
2. Establish the relations
   $\Delta = E \nabla$
   $\nabla=E^{-1}\Delta$
   $E^{\frac{1}{2}}\Delta=E^{\frac{1}{2}}\nabla=\delta$
   $\Delta\nabla=\nabla\Delta=\Delta-\nabla=\delta^2$
   $\mu\delta=\frac{1}{2}(\Delta+\nabla)$
   $E^{+\frac{1}{2}}=\mu \pm \frac{1}{2}\,\,\delta$
   $\mu^2=1+\frac{1}{4}\delta^2$
   $\mu=\frac{1}{2}(E^{\frac{1}{2}}+E^{-\frac{1}{2}})$
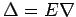
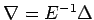
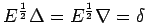
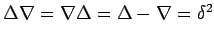
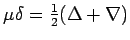
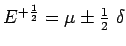
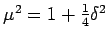
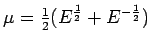
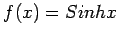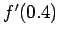3. From the following table of values of $f(x)=Sinhx$ find $f'(0.4)$ using central difference with h=0.001 and 0.002. which of these is the more accurate?
   

   x	Sinhx
   0.398	0.408591
   0.399	0.409671
   0.400	0.410752
   0.407	0.411834
   0.402	0.412915

4. Using Newton's forward difference formula, find an approximation to 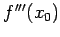$f'''(x_0)$ based on the points 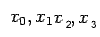and determine the error of this approximation.
5. Derive the error of the trapezoidal rule over the internal 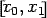by means of Taylor's theorem.
6. Determine h so that the trapezoidal rule will yield the value of
   
   $$I=\int\limits_{0}^{1}e^{-x^{2}}dx$$
   
   
   correct to six significant figures. Find the value of I using the computer.