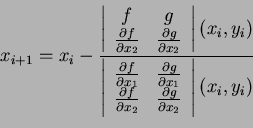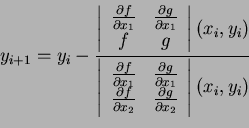Next: Bairstow Method
Up: ratish-1
Previous: Convergence of Newton-Raphson method:
Let 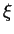 be a root of
be a root of 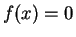 and
and 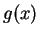 be an associated
iteration function. Say,
be an associated
iteration function. Say, 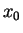 is the given starting point. Then
one can generate a sequence of successive approximations of
is the given starting point. Then
one can generate a sequence of successive approximations of 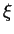 as:
This sequence
as:
This sequence
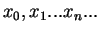 is said to converge to
is said to converge to
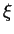 iff
iff
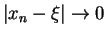 as
as
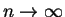 .
.
Now the natural question that would arise is what are the
conditions on
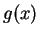 s.t. the sequence
s.t. the sequence
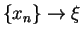 as
as 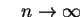
Here, we state few important comments on such a convergence:
(i)Suppose on an interval
![$ I=[a,b], \forall \,\, x \,\epsilon \,
I$](img247.png)
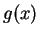 is defined and
is defined and
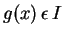 . i.e. g(x) maps
I into itself.
. i.e. g(x) maps
I into itself.
(ii) The iteration function 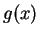 is continuous on I=[a,b].
is continuous on I=[a,b].
(iii)The iteration function g(x) is differentiable on ![$ I=[a,b]$](img249.png) and
and
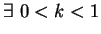 s.t.
s.t.
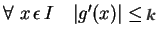
Theorem :
Let g(x) be an iteration function satisfying
(i), (ii) and (iii) then g(x) has exactly one fixed point 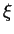 in
I and starting with any
in
I and starting with any
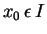 , the sequence
, the sequence
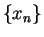 generated by fixed point iteration function converges to
generated by fixed point iteration function converges to
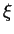 .
(you may refer to [ ] for proof).
.
(you may refer to [ ] for proof).
(iv) If
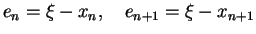 then
then
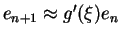 . For rapid convergence it is
desirable that
. For rapid convergence it is
desirable that 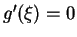 . Under this condition for the Newton
Raphson method one can show that
. Under this condition for the Newton
Raphson method one can show that
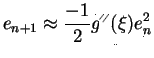 (i.e. quadratic
Convergence).
(i.e. quadratic
Convergence).
Remark: =1in =1 One can
generalize all the iterative methods for a system of nonlinear
equations. For instance, if we have two non-linear equations
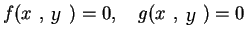 then given a
suitable starting point
then given a
suitable starting point
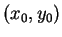 the
Newton-Raphson algorithm may be written as follows:
the
Newton-Raphson algorithm may be written as follows:
For i=1,2... until satisfied do



Next: Bairstow Method
Up: ratish-1
Previous: Convergence of Newton-Raphson method:
root
2006-02-07
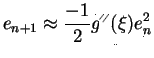 (i.e. quadratic
Convergence).
(i.e. quadratic
Convergence).
![]() then given a
suitable starting point
then given a
suitable starting point
![]() the
Newton-Raphson algorithm may be written as follows:
the
Newton-Raphson algorithm may be written as follows: