


Next: Bracketing Methods:
Up: ratish-1
Previous: ratish-1
Determination of roots of polynomials and transcendental equations
by Newton Raphson, Secant and Bairstow's method.
Motivation:
Let us look at a set of problems of scientific and engineering
interest to get a feel of what is root finding and why to find
roots. Later we learn how to find them.
Problem 1:
Suppose you are asked to cut a rectangular sheet
with one of its sides 1.25 mts longer than the other and the area
being 0.875
mts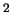 from a thin iron sheet of 5
mts
from a thin iron sheet of 5
mts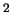 area. What
will be length of the 'smallest side'.
area. What
will be length of the 'smallest side'.
Say, length of the smallest side = 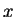
Length of the other side 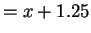
Area of rectangle
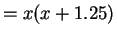
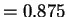 mt
mt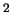
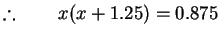
i.e.
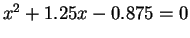
i.e. say
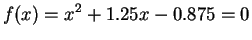 |
(1) |
So you need to solve a quadratic equation to find the required
quantity. i.e. You have to find the roots of a quadratic
equation.
You know that the roots of a quadratic equation
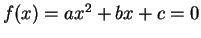 (2)
(2)
are given by
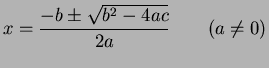 |
(3) |
Problem 2:
Concepts of thermodynamics are used extensively in their works by
say aerospace, mechanical and chemical engineers. Here, the
zero-pressure specific heat of dry air say 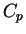 KJ/(KgK)
KJ/(KgK)
is related to temperature 'T' by.'
Now,
determine the temperature that corresponds to a specific heat of
1.2 KJ/(KgK). So, here you have to solve or find the
roots of
=1.2
i.e. find roots of
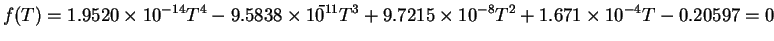 |
(4) |
Problem 3:
The concentration of pollutant bacteria 'C' in
a lake decreases as per the model:
Where 't' is the time variable. Determine the time required for
the bacteria concentration to be reduced to 9.
Here, you have to find the roots of
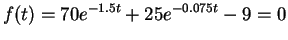 |
(5) |
Problem 4:
The volume of liquid in a hollow horizontal
cylinder of radius r and length L is related to the depth of the
liquid h by
Determine h given
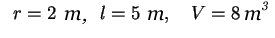
Here you
have to find the roots of
![$\displaystyle f(h)=5\times[2^{2}Cos^{-1}\left(\frac{2-h}{2}\right)-(2-h)\sqrt{2\times2\times h-h^{2}}]-8=0$](img19.png) |
(6) |
So you have seen that finding roots of 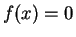 is very important
in finding solution to several scientific and engineering
problems.
is very important
in finding solution to several scientific and engineering
problems.
The equation 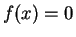 may be a polynomial equation or a
transcendental equation.
may be a polynomial equation or a
transcendental equation.
Polynomial Equations:
Polynomial equations in one
independent variable 'x' are a simple class of algebraic equations
that are represented as follows:
The 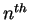 degree polynomial has
degree polynomial has 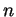 roots. They roots
may be real or complex.
roots. They roots
may be real or complex.
Examples:
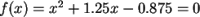
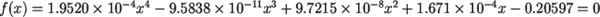
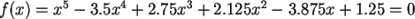
Transcendental Equation:
The equations include trigonometric or exponential or logarithmic functions.
Examples:
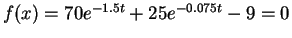
![$ f(x)=5x[4\cos^{-1}\left(\frac{2-x}{2}\right)-(2-x)\sqrt{4h-h^{2}}]-8=0$](img28.png)
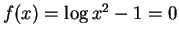
You may note that the example are nonlinear functions.
Method of solution:
Some of the ways of finding the roots or solution of 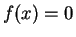 are:
are:
- Direct analytical methods
- graphical approach
- iterative methods etc.
Direct analytical methods: One may we able to find a
mathematical expression for the solution
(root) of 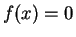 .
.
For example, for quadratic equations (2), we have solutions given
by (3). However a large number of equations cannot be solved by
direct
analytical methods.
Graphical Method: This approach involves plotting the
given function and determining the points where it crosses the
x-axis. These points, extracted approximately from the plot,
represent approximate values of the roots of the function.
Example:
Find the positive roots of
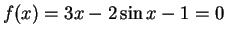
Rewrite
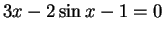 as
as
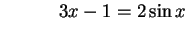
Now consider 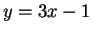 and
and
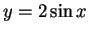 and plot them
and plot them
The x-co-ordinate of the point of intersection of 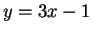 , and
, and
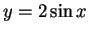 gives the required positive root of the given
function. Clearly thus approach is cumbersome and time consuming.
gives the required positive root of the given
function. Clearly thus approach is cumbersome and time consuming.
Iterative Methods: Starting with a initial guess solution
these methods generate a sequence of estimates to the solution
which is expected converge to the true solution. They are
grouped into two categories :
- Bracketing methods
- open methods
Bracketing Methods: These methods exploit the fact that a
function typically changes sign in the vicinity of a root. They
start with two initial guesses that bracket the root and then
systematically reduce the width of the bracket until the solution
to a desired accuracy is reached. The popular bracketing methods
are: (a) Bisection Method, (b) False Position (or) Regula Falsi
method, (c) Improved or
modified Regula Falsi Method.
Open methods: These methods are based on formulas that
require only a single starting (or guess) values of solution or
two starting values that do not necessarily bracket the root. They
may sometimes diverge or move away from true root as the
computation progresses. However when the open methods converge
they do so much more quickly than the Bracketing methods. Some of
the popular open methods are: (a) Secant method, (b)
Newton-Raphson method, (c) Bairstow's method (d) Muller's method
etc.
Subsections



Next: Bracketing Methods:
Up: ratish-1
Previous: ratish-1
root
2006-02-07
![]() (2)
(2)
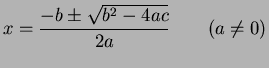
![$\displaystyle V=[r^{2}\quad \cos^{-1}\left(\frac{r-h}{r}\right)-(r-h)\sqrt{2rh-h^{2}}]L$](img17.png)
![$\displaystyle f(h)=5\times[2^{2}Cos^{-1}\left(\frac{2-h}{2}\right)-(2-h)\sqrt{2\times2\times h-h^{2}}]-8=0$](img19.png)
![]() , and
, and
![]() gives the required positive root of the given
function. Clearly thus approach is cumbersome and time consuming.
gives the required positive root of the given
function. Clearly thus approach is cumbersome and time consuming.