


Next: Interpolation:
Up: Curve Fitting : Interpolation,
Previous: Curve Fitting : Interpolation,
One of the
common tasks faced by scientists and engineers is the problem of
estimating the value of dependent variable 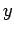 for an intermediate
value of the independent variable
for an intermediate
value of the independent variable 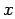 , given a table of discrete
data points
, given a table of discrete
data points
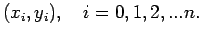 If We had a
function
If We had a
function 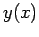 that passes through the given data points then we
can use it for evaluating
that passes through the given data points then we
can use it for evaluating 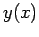 for the required value of
for the required value of 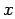 .
.
Can we construct such a function 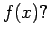
Yes we can and the process of constructing 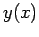 to fit the given
table of data points is called curve fitting.
to fit the given
table of data points is called curve fitting.
Depending upon the source from where the data is drawn, the value
of the data points may or may not be accurate. For instance, if
the data points are drawn from say, logarithmic or trigonometric
or interest or steam tables they are treated as accurate as these
tables are generated by using well behaved functions. On the
contrary the data drawn from experimental measurement tabulations
are prone to error's and are treated as not exact.
When the given data is exact then it is meaningful to construct
the function passing through the data points. The method of
constructing through the data points. The method of constructing a
function and estimating value at intermediate points is called
interpolation. The functions, thus constructed, are called as
interpolating polynomials.
Some of the common methods of interpolation are
- Lagrange Interpolation
- Newton's Interpolation
- Divided Difference Interpolation Formula
- Spline Interpolation, etc.
The Common strategy to deal with the inexact data is find an
approximate function that would represent the general trend of the
data, without necessarily passing through the individual points.
Linear and non-linear Least Square Regression has been a standard
approach in finding such approximating functions.
So, now we discuss about interpolation and later about Least
Square Regression process.



Next: Interpolation:
Up: Curve Fitting : Interpolation,
Previous: Curve Fitting : Interpolation,
root
2006-02-14