
Next: Computer Arithmetic.
Up : Main Previous:Computer Representation of Numbers
Numerical Errors:
Numerical errors arise during computations due to round-off errors and truncation errors.
Round-off Errors:
Round-off error occurs because computers use fixed number of bits and hence fixed number of binary digits to represent numbers. In a numerical computation round-off errors are introduced at every stage of computation. Hence though an individual round-off error due to a given number at a given numerical step may be small but the cumulative effect can be significant.
When the number of bits required for representing a number are less then the number is usually rounded to fit the available number of bits. This is done either by chopping or by symmetric rounding.
Chopping: Rounding a number by chopping amounts to
dropping the extra digits. Here the given number is truncated.
Suppose that we are using a computer with a fixed word length of
four digits. Then the truncated representation of the number ![]() will be
will be ![]() . The digits
. The digits ![]() will be dropped. Now to evaluate the error
due to chopping let us consider the normalized representation of
the given number
will be dropped. Now to evaluate the error
due to chopping let us consider the normalized representation of
the given number ![]() i.e.
i.e.
![]() chopping error in representing
chopping error in representing
![]() .
.
So in general if a number ![]() is the true value of a given
number and
is the true value of a given
number and
![]() is the normalized form of the
rounded (chopped) number
is the normalized form of the
rounded (chopped) number ![]() and
and
![]() is the
normalized form of the chopping error then
is the
normalized form of the chopping error then
![]()
Since
![]() , the chopping error
, the chopping error
![]()
Symmetric Round-off Error :
In the symmetric round-off method the last retained significant
digit is rounded up by 1 if the first discarded digit is greater
or equal to 5.In other words, if ![]() in
in ![]() is such that
is such that
![]() then the last digit in
then the last digit in ![]() is raised by 1
before chopping
is raised by 1
before chopping
![]() . For example let
. For example let
![]() be two given numbers to be rounded to
five digit numbers. The normalized form x and y are
be two given numbers to be rounded to
five digit numbers. The normalized form x and y are
![]() and
and
![]() . On rounding
these numbers to five digits we get
. On rounding
these numbers to five digits we get
![]() and
and
![]() respectively. Now w.r.t
respectively. Now w.r.t ![]() here
here
![]()
![]()
In either case error
![]() .
.
Truncation Errors:
Often an approximation is used in place of an exact mathematical
procedure. For instance consider the Taylor series expansion of
say ![]() i.e.
i.e.
![]()
Practically we cannot use all of the infinite number of terms in the series for computing the sine of angle x. We usually terminate the process after a certain number of terms. The error that results due to such a termination or truncation is called as 'truncation error'.
Usually in evaluating logarithms, exponentials, trigonometric
functions, hyperbolic functions etc. an infinite series of the
form
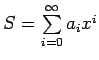 is replaced by a
finite series
is replaced by a
finite series
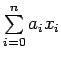 . Thus a truncation
error of
. Thus a truncation
error of
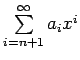 is introduced
in the computation.
is introduced
in the computation.
For example let us consider evaluation of exponential function
using first three terms at ![]()
![]()
![]()
![]()
Truncation Error
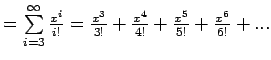
![]()
![]()
![]()
![]()
Absolute and Relative Errors:
Absolute Error: Suppose that ![]() and
and ![]() denote the true
and approximate values of a datum then the error incurred on
approximating
denote the true
and approximate values of a datum then the error incurred on
approximating ![]() by
by ![]() is given by
is given by
![]()
and the absolute error ![]() i.e. magnitude of the error is
given by
i.e. magnitude of the error is
given by
![]()
Relative Error: Relative Error or normalized
error ![]() in representing a true datum
in representing a true datum ![]() by an
approximate value
by an
approximate value ![]() is defined by
is defined by
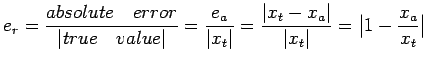
and
![]()
Sometimes ![]() is defined by
is defined by
![]()
![]() If
If
![]() and
and
![]() then
then
![]()
![]()
![]()
![]()
Machine Epsilon: Let us assume that we have a decimal computer system.
We know that we would encounter round-off error when a number is represented in floating-point form. The relative round-off error due to chopping is defined by
![]()
Here we know that
![]()
![]()
i.e. maximum relative round-off error due to chopping is given by
![]() . We know that the value of 'd' i.e the length of
mantissa is machine dependent. Hence the maximum relative
round-off error due to chopping is also known as machine epsilon
. We know that the value of 'd' i.e the length of
mantissa is machine dependent. Hence the maximum relative
round-off error due to chopping is also known as machine epsilon
![]() . Similarly , maximum relative
round-off error due to symmetric rounding is given by
. Similarly , maximum relative
round-off error due to symmetric rounding is given by
![]()
Machine-Epsilon
![]() for symmetric rounding is given
by,
for symmetric rounding is given
by,
![]()
It is important to note that the machine epsilon represents upper bound for the round-off error due to floating point representation.
For a computer system with binary representation the machine epsilon due to chopping and symmetric rounding are given by
![]()
respectively.
Eg: Assume that our binary machine has 24-bit mantissa. Then
![]() . Say that our system
can represent a q decimal digit mantissa.
. Say that our system
can represent a q decimal digit mantissa.
Then,
![]()
i.e
![]()
![]()
![]()
![]() that our machine can store numbers with seven
significant decimal digits.
that our machine can store numbers with seven
significant decimal digits.
Next: Computer Arithmetic. Up : Main Previous:Computer Representation of Numbers