In this section, we will look at some special classes of square
matrices which are diagonalisable. We will also be dealing with
matrices having complex entries and hence for a matrix
![$ A=[a_{ij}],$](img31.png) recall the following definitions.
recall the following definitions.
Note that a symmetric matrix is always Hermitian, a skew-symmetric matrix
is always skew-Hermitian and an orthogonal matrix is always
unitary. Each of these matrices are normal. If  is a unitary
matrix then
is a unitary
matrix then
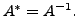
EXAMPLE 6.3.2
- Let
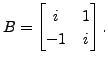 Then
Then 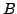 is skew-Hermitian.
is skew-Hermitian.
- Let
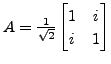 and
and
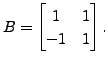 Then
Then  is a unitary matrix and
is a unitary matrix and 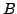 is a normal
matrix. Note that
is a normal
matrix. Note that
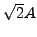 is also a normal matrix.
is also a normal matrix.
EXERCISE 6.3.4
- Let
 be a square matrix such that
be a square matrix such that 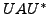 is a diagonal matrix for some unitary matrix
is a diagonal matrix for some unitary matrix 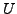 .
Prove that
.
Prove that  is a normal matrix.
is a normal matrix.
- Let
 be any matrix. Then
be any matrix. Then
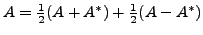 where
where
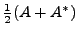 is the Hermitian part of
is the Hermitian part of  and
and
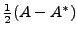 is the skew-Hermitian part of
is the skew-Hermitian part of 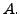
- Every matrix can be uniquely expressed as
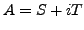 where both
where both 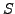 and
and  are Hermitian matrices.
are Hermitian matrices.
- Show that
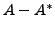 is always skew-Hermitian.
is always skew-Hermitian.
- Does there exist a unitary matrix
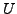 such that
such that
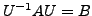 where
where
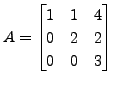 and
and
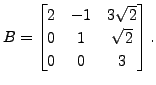
Proof.
Let
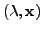
be an eigenpair. Then
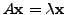
and
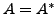
implies
Hence
But
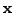
is an eigenvector and hence
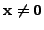
and so the real number
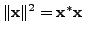
is non-zero as well. Thus
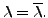
That is,
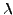
is a real number.
height6pt width 6pt depth 0pt
Proof.
We will prove the result by induction on the size of
the matrix. The result is clearly true if
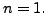
Let the result
be true for
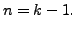
we will prove the result in case
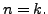
So, let

be a
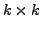
matrix and let
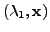
be
an eigenpair of

with
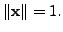
We now extend the linearly
independent set
to form an orthonormal basis
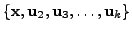
(using
Gram-Schmidt
Orthogonalisation) of
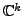
.
As
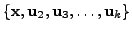 is an orthonormal set,
is an orthonormal set,
Therefore, observe that for all
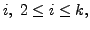
Hence, we also have
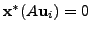
for
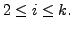
Now, define
![$ U_1 = [ {\mathbf x}, \; {\mathbf u}_2, \; \cdots, {\mathbf u}_k ]$](img3023.png)
(with
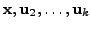
as columns of
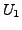
). Then the matrix
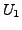
is a unitary matrix
and
where
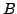
is a
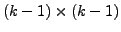
matrix. As
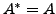
,we get
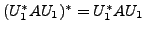
. This condition,
together with the fact that
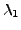
is a real number (use Proposition
6.3.5), implies that
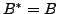
. That is,
is also
a Hermitian matrix. Therefore, by induction hypothesis there
exists a
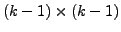
unitary matrix
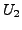
such that
Recall that , the entries
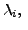
for
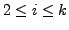
are the eigenvalues of the matrix
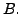
We also know that
two similar matrices have the same set of eigenvalues. Hence, the
eigenvalues of

are
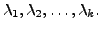
Define
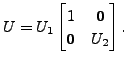
Then
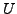
is a unitary matrix
and
Thus,
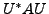
is a diagonal matrix with diagonal entries
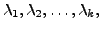
the eigenvalues of
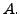
Hence, the result follows.
height6pt width 6pt depth 0pt
COROLLARY 6.3.7
Let  be an
be an
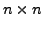 real symmetric matrix. Then
real symmetric matrix. Then
- the eigenvalues of
 are all real,
are all real,
- the corresponding eigenvectors can be chosen to have real entries, and
- the eigenvectors also form an orthonormal basis of
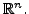
Proof.
As

is symmetric,

is also an Hermitian matrix. Hence, by Proposition
6.3.5, the eigenvalues of

are all real.
Let
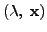
be an eigenpair of
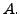
Suppose

Then there exist
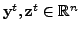
such that
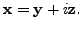
So,
Comparing the real and imaginary parts, we get
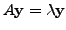
and
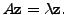
Thus, we can choose the eigenvectors to have real entries.
To prove the orthonormality of the eigenvectors, we proceed on the lines
of the proof of Theorem 6.3.6, Hence, the readers are advised
to complete the proof.
height6pt width 6pt depth 0pt
Remark 6.3.9
In the previous exercise, we saw that the matrices
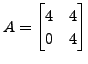 and
and
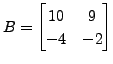 are similar but not unitarily equivalent, whereas
unitary equivalence implies similarity equivalence as
are similar but not unitarily equivalent, whereas
unitary equivalence implies similarity equivalence as
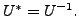 But in numerical calculations, unitary transformations are preferred
as compared to similarity transformations. The main reasons being:
But in numerical calculations, unitary transformations are preferred
as compared to similarity transformations. The main reasons being:
- Exercise 6.3.8.2 implies
that an orthonormal
change of basis leaves unchanged the sum of squares of the
absolute values of the entries which need not be true under a
non-orthonormal change of basis.
- As
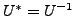 for a unitary matrix
for a unitary matrix 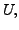 unitary equivalence is
computationally simpler.
unitary equivalence is
computationally simpler.
- Also in doing ``conjugate transpose", the loss of accuracy due to round-off
errors doesn't occur.
We next prove the Schur's Lemma and use it to show that normal matrices
are unitarily diagonalisable.
LEMMA 6.3.10 (Schur's Lemma)
Every
 complex matrix is unitarily similar to an upper
triangular matrix.
complex matrix is unitarily similar to an upper
triangular matrix.
Proof.
We will prove the result by induction on the size of
the matrix. The result is clearly true if
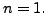
Let the result
be true for
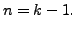
we will prove the result in case
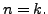
So, let

be a
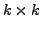
matrix and let
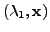
be
an eigenpair for

with
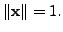
Then the linearly
independent set
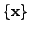
can be extended, using the
Gram-Schmidt
Orthogonalisation process, to get an orthonormal basis
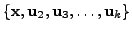
of
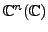
. Then
![$ U_1 = [ {\mathbf x}\; {\mathbf u}_2 \; \cdots {\mathbf u}_k ]$](img3081.png)
(with
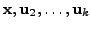
as the columns of the matrix
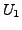
)
is a unitary matrix and
where
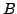
is a
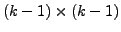
matrix. By induction
hypothesis there exists a
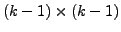
unitary matrix
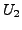
such that
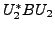
is an upper triangular matrix
with diagonal entries
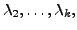
the eigen
values of the matrix
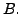
Observe that since the eigenvalues of
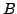
are
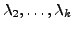
the
eigenvalues of

are
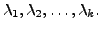
Define
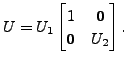
Then check that
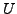
is a unitary matrix and
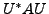
is an upper triangular matrix with diagonal entries
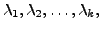
the eigenvalues of the
matrix
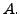
Hence, the result follows.
height6pt width 6pt depth 0pt
We end this chapter with an application of the theory of diagonalisation
to the study of conic sections in analytic geometry and the study of
maxima and minima in analysis.
A K Lal
2007-09-12
![]() recall the following definitions.
recall the following definitions.
![]()
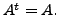
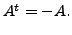
![]() is a unitary
matrix then
is a unitary
matrix then
![]()
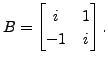 Then
Then 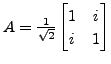 and
and
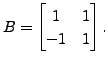 Then
Then ![]() as
as ![]() is a unitary matrix. So,
is a unitary matrix. So, ![]() is unitarily
similar to the matrix
is unitarily
similar to the matrix ![]() .
.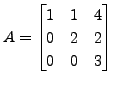 and
and
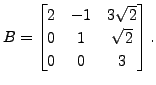
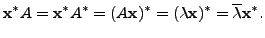
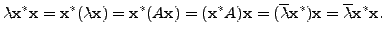
![]() form an orthonormal
basis of
form an orthonormal
basis of
![]()
 .
.
![]() is an orthonormal set,
is an orthonormal set,
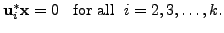
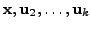 as columns of
as columns of 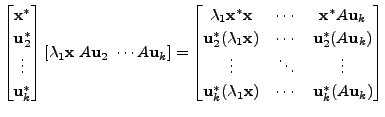
![$\displaystyle \left[\begin{array}{c\vert c} \lambda_1 & {\mathbf 0}\\ \hline {\mathbf 0}& \\
\vdots & B \\ {\mathbf 0}& \end{array} \right],$](img3029.png)
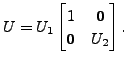 Then
Then 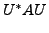
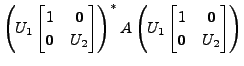
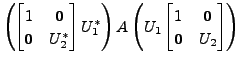
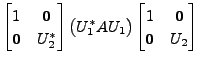
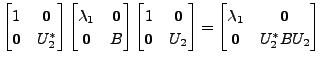
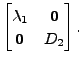
 Then there exist
Then there exist
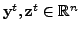 such that
such that
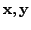 corresponding to distinct eigenvalues
corresponding to distinct eigenvalues
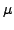 satisfy
satisfy
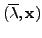 is
an eigenpair for
is
an eigenpair for 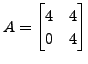 and
and
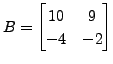 are similar. Is it possible to find a unitary
matrix
are similar. Is it possible to find a unitary
matrix 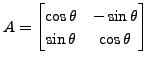 for some
for some
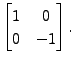
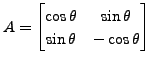 for some
for some
![]() In this case, prove that
In this case, prove that ![]() reflects the vectors
in
reflects the vectors
in
![]() about a line passing through origin. Also, determine this line.
about a line passing through origin. Also, determine this line.
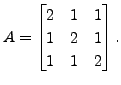 Determine
Determine 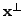 is a two dimensional rotation of
is a two dimensional rotation of
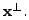
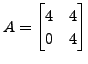 and
and
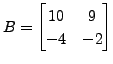 are similar but not unitarily equivalent, whereas
unitary equivalence implies similarity equivalence as
are similar but not unitarily equivalent, whereas
unitary equivalence implies similarity equivalence as
![$\displaystyle \begin{bmatrix}{\mathbf x}^* \\ {\mathbf u}_2^* \\ \vdots \\ {\ma...
..._1 & * \\ \hline {\mathbf 0}& \\ \vdots & B \\ {\mathbf 0}&
\end{array} \right]$](img3082.png)
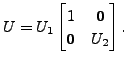 Then check that
Then check that 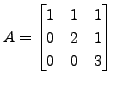 and
and
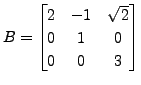 are unitarily equivalent via the unitary matrix
are unitarily equivalent via the unitary matrix
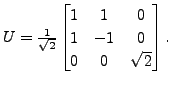 Hence, conclude that
the upper triangular matrix obtained in the "Schur's Lemma" need
not be unique.
Hence, conclude that
the upper triangular matrix obtained in the "Schur's Lemma" need
not be unique.