Next: Difference Operator Up: Newton's Interpolation Formulae Previous: Newton's Interpolation Formulae Contents
In many practical situations, for a function ![]() which
either may not be explicitly specified or may be difficult to handle,
we often have a tabulated data
which
either may not be explicitly specified or may be difficult to handle,
we often have a tabulated data
![]() where
where
![]() and
and
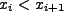 for
for
![]() In such cases, it may be required to
represent or replace the given function by a simpler function, which
coincides with the values of
In such cases, it may be required to
represent or replace the given function by a simpler function, which
coincides with the values of ![]() at the
at the ![]() tabular points
tabular points
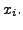 This process is known as INTERPOLATION. Interpolation is
also used to estimate the value of the function at the non tabular
points. Here, we shall consider only those functions which are
sufficiently smooth, i.e., they are differentiable sufficient number
of times. Many of the interpolation methods, where the tabular
points are equally spaced, use difference operators. Hence, in the
following we introduce various difference operators and
study their properties before looking at the interpolation
methods.
This process is known as INTERPOLATION. Interpolation is
also used to estimate the value of the function at the non tabular
points. Here, we shall consider only those functions which are
sufficiently smooth, i.e., they are differentiable sufficient number
of times. Many of the interpolation methods, where the tabular
points are equally spaced, use difference operators. Hence, in the
following we introduce various difference operators and
study their properties before looking at the interpolation
methods.
We shall assume here that the TABULAR POINTS
![]() are equally spaced, i.e.,
are equally spaced, i.e.,
![]() for each
for each
![]() The real number
The real number ![]() is called the STEP LENGTH.
This gives us
is called the STEP LENGTH.
This gives us
![]() Further,
Further,
![]() gives the value of the function
gives the value of the function ![]() at the
at the
![]() tabular point.
The points
tabular point.
The points
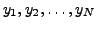 are known as
NODES or NODAL VALUES.
are known as
NODES or NODAL VALUES.
A K Lal 2007-09-12