We start with a few simple examples:

Example 1: A person is holding a 100N weight (that is roughly a 10kg mass) by a light weight (negligible mass) rod AB. The rod is 1.5m long and weight is hanging at a distance of 1m from the end A, which is on a table (see figure 6). How much force should the person apply to hold the weight?

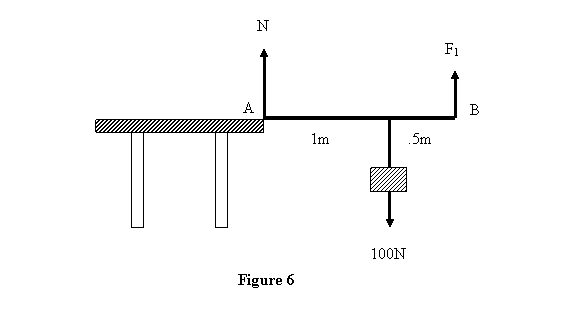
Let the normal reaction of the table on the rod be N and the force by the point be F₁. Then the two equilibrium conditions give

 

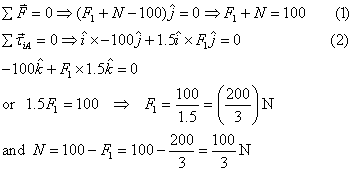
Example 2: As the second illustration we take the example of a lever that you may have used sometime or the other. We are trying to lift a 1000N (~100kg mass) weight by putting a light weight but strong rod as shown in the figure using the edge of a brick as the fulcrum. The height of the brick is 6cm. The question we ask is: what is the value of the force applied in the vertical direction that is needed to lift the weight? Assume the brick corner to be rough so that it provides frictional force.

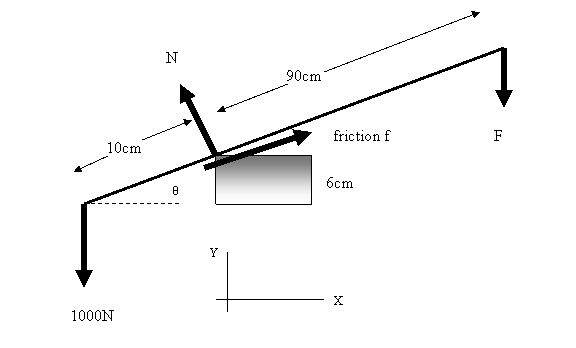
(Note: If the brick did not provide friction, the force applied cannot be only in the vertical direction as that would not be sufficient to cancel the horizontal component of N). Let us see what happens if the brick offered no friction and we applied a force in the vertical direction. The fulcrum applies a force N perpendicular to the rod so if we apply only a vertical force, the rod will tend to slip to the left because of the component of N in that direction. Try it out on a smooth corner and see that it does happen. However, if the friction is there then the rod will not slip. Let us apply the equilibrium conditions in such a situation. The balance of forces gives

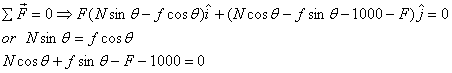
Let us choose the fulcrum as the point about which we balance the torque. It gives

Then

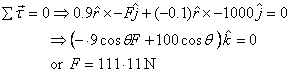
The normal force and the frictional force can now be calculated with the other two equations obtained above by the force balance equation.

In the example above, we have calculated the torques and have also used normal force applied on a surface. We are going to encounter these quantities again and again in solving engineering problems. So let us study each one of them in detail.

Torque due to a force: As discussed earlier, torque about a point due to a force 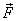is obtained as the vector product

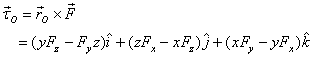
where 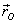is a vector from the point O to the point where the force is being applied. Actually 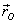could be a vector from O to any point along the line of action of the force as we will see below. The magnitude of the torque is given as

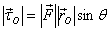
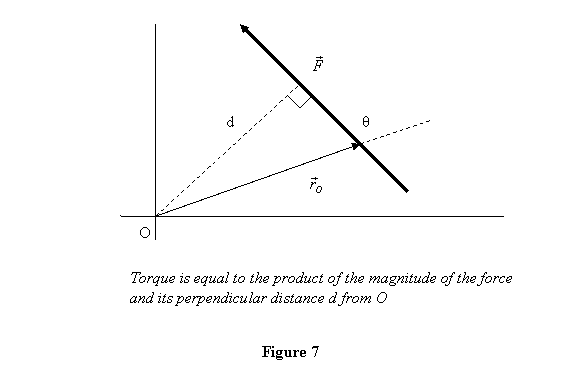
Thus the magnitude of torque is equal to the product of the magnitude of the force and the perpendicular distance 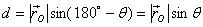from O to the line of action of the force as shown in figure 7 in the plane containing point O and the force vector. Since this distance is fixed, the torque due to a force can be calculated by taking vector 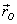to be any vector from O to the line of action of the force. The unit of a torque is Newton-meter or simply Nm.

Let us look at an example of this in 2 dimensions.

Example 3: Let there be a force of 20 N applied along the vector going from point (1,2) to point (5,3). So the force can be written as its magnitude times the unit vector from (1,2) to (5,3). Thus

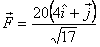
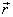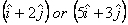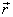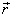Torque can be calculated about O by taking to be either . As argued above, the answer should be the same irrespective of which we choose. Let us see that. By taking to be 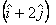we get

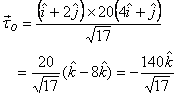
On the other hand, with 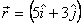we get

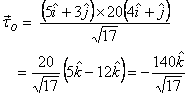
Which is the same as that obtained with 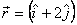. Thus we see that the torque is the same no matter where along the line of action is the force applied. This is known as the transmissibility of the force. So we again write that

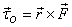
where 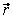is any vector from the origin to the line of action of the force.

If there are many forces applied on a body then the total moment about O is the vector sum of all other moments i.e.

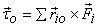
As a special case if the forces are all applied at the same point j then

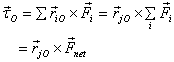
This is known as Varignon's theorem. Its usefulness arises from the fact that the torque due to a given force can be calculated as the sum of torques due to its components.

As would be clear to you from the discussion so far torque depends on the location of point O . If for the same applied force, the torque is taken about a different point, the torque would come out to be different. However, as mentioned earlier, there is one special case when the torque is independent of the force applied and that is when the net force(vector sum of all forces) on the system is zero. Let us prove that now: Consider the torque of a force being calculated about two different points O and O' (figure 8).

 

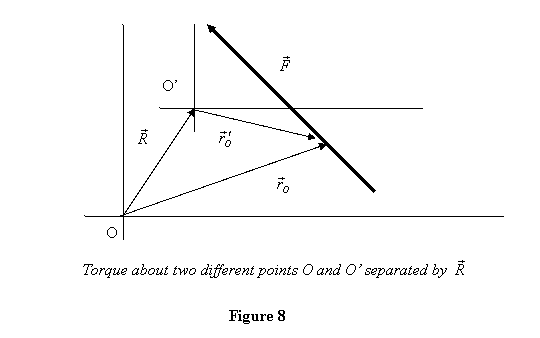
The torques about O and O' and their difference is:

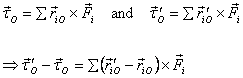
But from the figure above

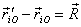
Therefore

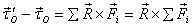
Now if the net force is zero, 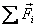is zero and the difference between the torques about two different points also vanishes. A particular example of the net force being zero is two equal magnitude forces in directions opposite to each other and applied at a distance from one another, as in figure 5 above and also shown in figure 9 below. This is known as a couple and the corresponding torque with respect to any point is given as

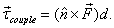
where 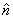is a unit vector perpendicular to the forces coming out of the space between them and d is the perpendicular distance between the forces (see figure 9).

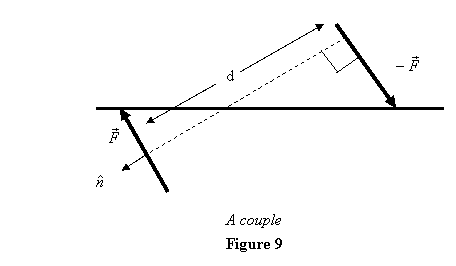
Since the net force due to a couple is zero, the only action a couple has on a body is to tend to rotate it. Further the moment of a couple is independent of the origin, and so it can be applied anywhere on the body and it will have the same effect on the body. We can even change the magnitude of the force and alter the distance between them keeping the magnitude of the couple the same. Then also the effect of couple will be the same. Such vectors whose effect remains unchanged irrespective of where they are applied are known as free vectors. Free vectors have a nice property that they can be added irrespective of where they are applied without changing the effect they produce. Thus a couple is a free vector (Is force a free vector?). It is represented by the symbols

 

with the arrows clearly giving the sense of rotation. Keep in mind though that the direction of the couple (in the vector sense) is perpendicular to the plane in which the forces forming the couple are.

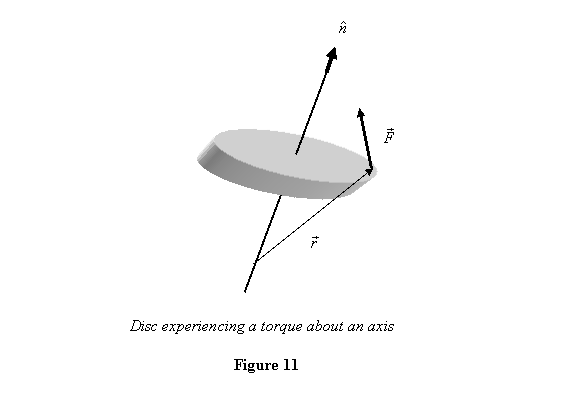
Next we focus on the moment of a force about an axis.

Moment of force about an axis: So far we have talked about moment of a force about a point only. However, many a times a body rotates about an axis. This is the situations you have bean studying in you 12^th grade. For example a disc rotating about an axis fixed in two fixed ball bearings. In this case what affects the rotation is the component of the torque along the axis, where the torque is taken about a point O (the point can be chosen arbitrarily) on the axis as given in figure 11. Thus

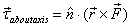
where 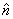is the unit vector along the axis direction and 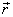is the vector from point O on the axis to the force .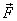

Using vector identities (exercise at the end of Lecture 1), it can also be written as

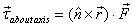
Thus the moment of a force about an axis is the magnitude of the component of the force in the plane perpendicular to the axis times its perpendicular distance from the axis. Thus if a force is pointing towards the axis, the torque generated by this force about the axis would be zero. This can be understood as follows. When a force is applied, forces are generated at the ends of the axis being held on a one place. These forces together with generate the torque when components along the axis by responsible for rotation of the body about the axis, in the same manner, the couple about the axis is given by the component of the couple moment in the direction for the axis. You can work it out; it is actually equal to the component of the force in the plane perpendicular to the axis times the distance of the force line of action from the axis. One point about the moment about an axis, it is independent of the origin since it depends only on the distance of the force the axis.

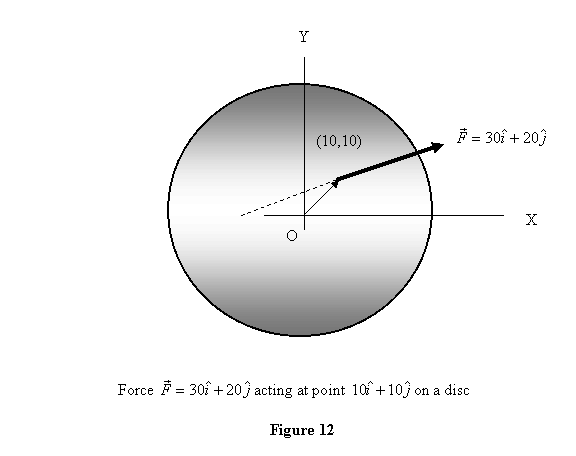
As an example let us consider a disc of radius 30 cm with its axis along the z-axis and its centre at z=0. Let a force 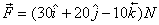act on it at the point 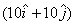on the disc. We now find its moment about its axis. The axis has 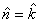. We take the origin at the centre of the disc to calculate

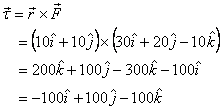
Therefore the torque about the z-axis is

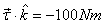
Thus the torque about the axis is in the negative z direction which means that it would tend to rotate the disc clockwise.

Let us now see if it fits with our conventional way of calculating torque of a force about an axis. For the force 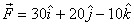  the z-component of the force will not give any torque about the z-axis because it cannot rotate the body about the z-axis. So the only component of the force that gives torque about the z-axis is 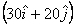that acts on the point as shown in figure 12. The magnitude of this force is .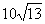

The equation of line along which the force acts is

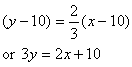
To find the perpendicular distance of this line from the origin, we consider a line perpendicular to this line 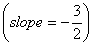passing through the origin and consider the point where it intersects with . The perpendicular line is

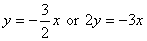
Solving for the intersection point we get

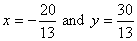
which gives the perpendicular distance of the line of force from the centre to be

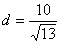
Then torque about z-axis therefore is therefore 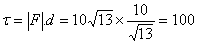clockwise, which is the same as obtained that earlier. I would like you to notice that even in this simple example using vector algebra makes life quite easy.