Example1: A person walks
300m to the east and 400m to the north to reach his friend's
house. What is the total displacement of the person, and
what is the total distance traveled by him?
Recall that distance is a scalar quantity. Thus the total distance covered is 700m. Displacement, on the other hand, is a vector quantity so to find the net displacement, we add the two vectors to get a displacement of 500m at an angle 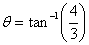 from east to north (Figure 7). from east to north (Figure 7).
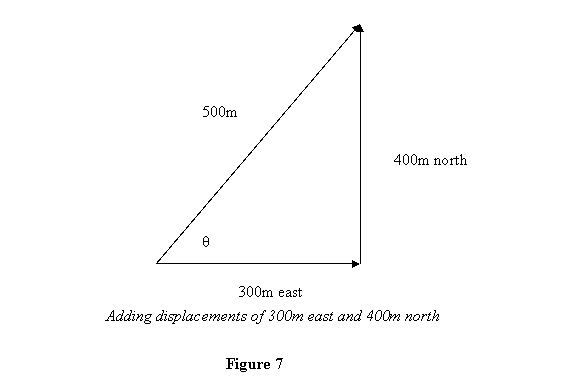
Example 2 : Two persons are pushing a box so that the net force on the box is 12N to the east If one of the person is applying a force 5N to the north, what is the force applied by the other person.
Let the force by person applying 5N be
denoted by 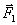 and
that by the other person by and
that by the other person by  .
We then have .
We then have
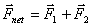
so that
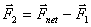
Solution for 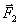 is given graphically in figure 8. The force comes out to be 13N at an angle of is given graphically in figure 8. The force comes out to be 13N at an angle of 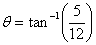 from east to south. from east to south.
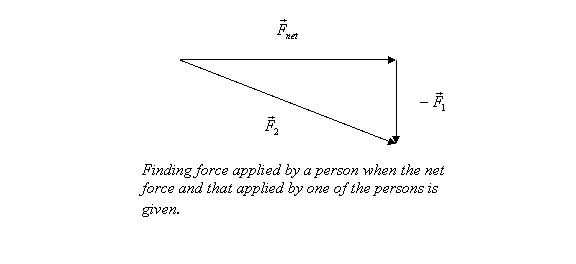 Figure
8 Figure
8
Although graphical way is nice to visualize
vectors in two dimensions, it becomes difficult to
work with it in three dimensions, and also when many
vectors and many operations with them are involved.
So vector algebra is best done by representing them
in terms of their components along the x, y & z
axes in space. We now discuss how to this is done.
To represent vectors in terms of their x,y and z components, let us first introduce the concept of unit vector. A unit vector 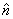 in
a particular direction is a vector of magnitude '1'
in that direction. So a vector in that particular direction
can be written as a number times the unit vector in
a particular direction is a vector of magnitude '1'
in that direction. So a vector in that particular direction
can be written as a number times the unit vector 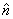 . Let us denote the unit vector in x-direction as . Let us denote the unit vector in x-direction as 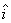 , in y-direction as , in y-direction as 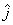 and in z-direction as and in z-direction as 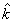 . Now any vector can be described as a sum of three vectors . Now any vector can be described as a sum of three vectors 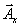 , , 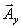 and and 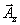 in the directions x, y and z, respectively, in any order (recall that order does not matter because vector sum is commutative). Then a vector in the directions x, y and z, respectively, in any order (recall that order does not matter because vector sum is commutative). Then a vector
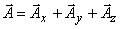
Further, using the concept of unit vectors, we can write 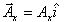 , where Ax is a number. Similarly , where Ax is a number. Similarly 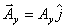 and and 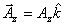 . So the vector above can be written as . So the vector above can be written as
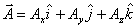
where Ax, Ay and Az are
known as the x, y, & z components of the vector.
For example a vector 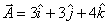 would
look as shown in figure 9. would
look as shown in figure 9.
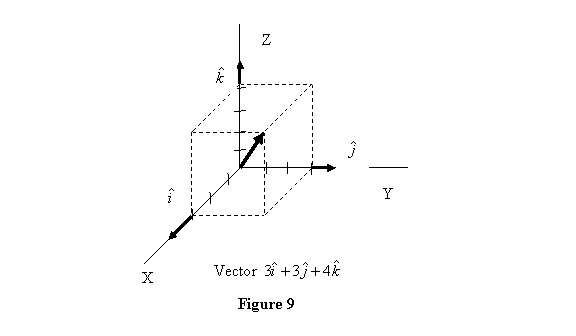
It is clear from figure 9 that the magnitude of the vector 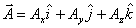 is is 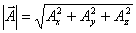 . Now when we add two vector, say . Now when we add two vector, say 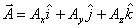 and and 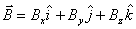 , all we have to do is to add their x-components, y-components and the z-components and then combine them to get , all we have to do is to add their x-components, y-components and the z-components and then combine them to get
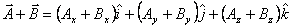
Similarly multiplying a vector by a number is same as increasing all its components by the same amount. Thus
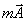 = = 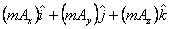
How about the multiplying by -1? It just changes the sign of all the components. Putting it all together we see that
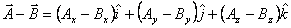
Having done the addition and subtraction of two vectors, we now want to look at the product of two vectors. Let us see what all possible products do we get when we multiply components of two vectors. By multiplying all components with one another, we have in all nine numbers shown below:
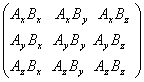
The question is how do we define the product of two vectors from the nine different numbers obtained above? We will delay the answer for some time and come back to this question after we establish the transformation properties of scalars and vectors. By transformation properties we mean how does a scalar quantity or the components of a vector quantity change when we look at them from a different (rotated) frame?
Let us first look at a scalar quantity.
As an example, we take the distance traveled by a person.
If we say that the distance covered by a person in
going from one place to another is 1000m in one frame,
it remains the same irrespective of whether we look
at it from the frame (xy ) or in a frame (x'
y' ) rotates
about the z-axis (see figure 10).
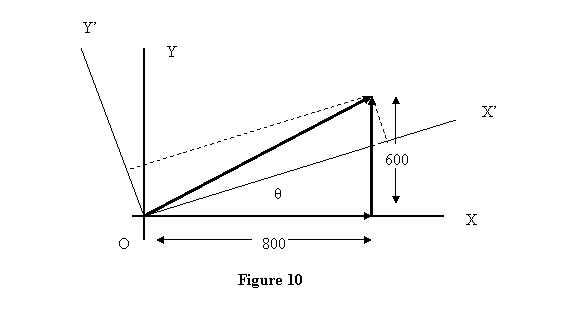
Let us now say that a person moves
800 meter along the x-axis and 600 meters along the
y-axis so that his net displacement is a vector of
1000m in magnitude at an angle of from the x-axis as
shown in figure 10. The total distance traveled by
the person is 1400m. Now let us look at the same situation
frame different frame which has its x' & y' axis rotated about the z- axis. Note that the total distance traveled by the person (a scalar quantity) remains the same, 1400m, in both the frames. Further, whereas the magnitude of the displacement & its
direction in space remains unchanged, its components
along the x' and y' axis, shown by dashed lines in
figure 10, are now different. Thus we conclude the
scalar quantity remains unchanged when seen from a
rotational frame. The component of a given vector are
however different in the rotated frame, as demonstrated
by the example above. Let us now see how the components
in the original frame and the rotated frame are related.
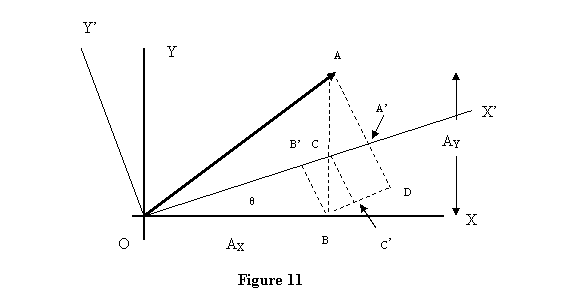
In figure 11, OA is a vector with Ax =
OB , Ay = AB, Ax' = OA' and Ay' =
AA'. Using the dashed lines drawn in the figure, we obtain
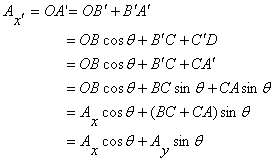
Similarly
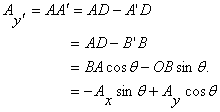
So we learn that if the same vector
is observed from a frame obtained by a rotation about
the z-axis by an angle θ, its x and y components
in the new frame are
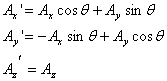
One can similarly define how components mix when rotation is about the y or the x- axis. Under the y axis rotation
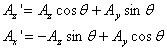
And under a rotation about the x-axis
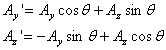
Let us summarize the results obtained above:
- Scalar quantity is specified by a number and that number remains the same in two different frames rotated with respect to each other.
- A vector quantity is specified by its components along the x, y, and the z axes and when seen from another frame rotated with respect to a given frame, these components change according to the rules derived above.
We are now ready to get back to defining the product of two vectors. Recall that we had a collection of nine quantities:
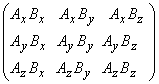
We are now going to mix these quantities in such a manner that one combination will give a scalar quantity whereas the other one will give us a vector quantity. This then defines the scalar and vector product of two vectors.
|