Modulus of a Complex Number: The absolute value or modulus of a complex number ![]() is denoted by
is denoted by ![]() and is given by
and is given by
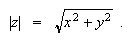
Here, as usual, the radical stands for the principal (non-negative) square root of ![]() .
.
Note that ![]() is always a non-negative real number and that the only complex number whose modulus is zero is the number
is always a non-negative real number and that the only complex number whose modulus is zero is the number ![]() . Basically the above definition extends the concept of absolute value of a real number
. Basically the above definition extends the concept of absolute value of a real number ![]() to the complex number system.
to the complex number system.
Example: The modulus of the complex number ![]() is
is ![]() .
.
Properties:
1.
![]() and
and ![]() iff
iff ![]() .
.
2. ![]() .
.
3.
![]() .
.