Q. Mark the following statements as true/false. Check to evaluate and then click at explanation to see the answer. |
| Sr.No |
Quiz |
Options |
Correct Answers |
Reasoning |
1.
|
For a function 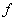 , for its limit to exist at , for its limit to exist at 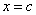 , , 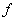 must be defined at must be defined at 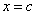 . .
|
True
False
|
|
|
2.
|
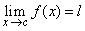 means that there exists a sequence means that there exists a sequence 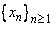 in the domain of in the domain of 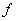 such that such that 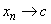 and and 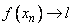 . . |
True
False
|
|
|
3.
|
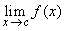 does not exists means that for every sequence does not exists means that for every sequence 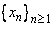 in the domain of in the domain of 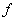 with with 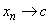 but but 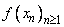 is not convergent is not convergent
|
True
False
|
|
|
4.
|
For a function 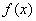 if there exists a sequence if there exists a sequence 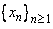 in domain of in domain of 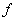 such that such that 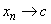 but but 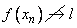 then then 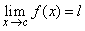 does not exist. does not exist.
|
True
False
|
|
|
5.
|
Saying that for a function 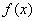 , , 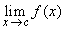 does not exists means: for every does not exists means: for every 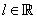 for every for every 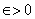 there exists there exists 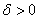 such that such that 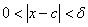 but but 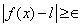
|
True
False
|
|
|