Q. Mark the following statements as true/false. Check to evaluate and then click at explanation to see the answer. |
| Sr.No |
Quiz |
Options |
Correct Answers |
Reasoning |
1.
|
Let 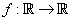 be a differentiable function such that be a differentiable function such that 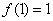 and and 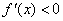 for for 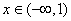 and and 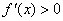 for for 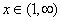 . Then . Then 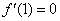 and and 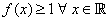 . .
|
True
False
|
|
|
2.
|
Both functions 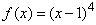 and and 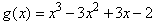 have local extreme at have local extreme at 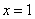 . . |
True
False
|
|
|
3.
|
Let 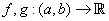 be such that both have a relative maximum at be such that both have a relative maximum at 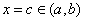 . Then . Then 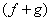 also has a local maximum at also has a local maximum at 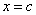 . .
|
True
False
|
|
|
4.
|
Let 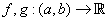 be such that both have a local minimum at be such that both have a local minimum at 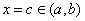 . Then . Then 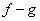 also has a local minimum at also has a local minimum at 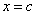 . .
|
True
False
|
|
|
5.
|
Let 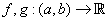 be such that both be such that both 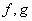 have a local maximum at have a local maximum at 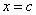 . Then . Then 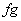 also has a local maximum at also has a local maximum at 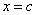 . .
|
True
False
|
|
|
6.
|
Let
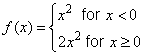
Then the 2nd derivative test can be applied to 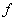 to deduce it has local minimum at to deduce it has local minimum at 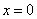 . . |
True
False
|
|
|
7.
|
Let 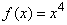 . Then the second derivative test can be applied to . Then the second derivative test can be applied to 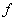 to deduce that to deduce that 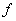 has local minimum at has local minimum at 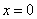 . .
|
True
False
|
|
|
8.
|
Let 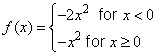
Then the first derivative test applies to 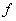 and hence it has a local maximum at and hence it has a local maximum at 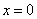 . . |
True
False
|
|
|