For a continuous function 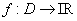 where where 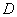 is a cubical region is a cubical region
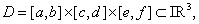
the triple integral of 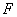 over over 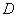 , denoted by , denoted by
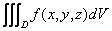
can be defined in a manner similar to that of the double integral. We divide the region 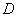 into into 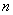 rectangular cells rectangular cells 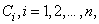 where the volume of the where the volume of the 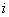 th cell is th cell is 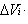 We select any arbitrary point We select any arbitrary point 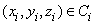 and consider the limit of the (Riemann) sums and consider the limit of the (Riemann) sums
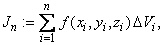
the limit being taken as 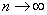 with with 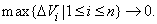 The triple integral is this limit, whenever it exists. As in the two variables case, this can be extended to closed bounded regions The triple integral is this limit, whenever it exists. As in the two variables case, this can be extended to closed bounded regions 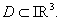 We omit the details. The triple integral is also written as We omit the details. The triple integral is also written as
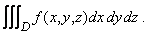
Triple integral satisfies properties similar to the ones satisfied by double integrals, see theorem 40.1.3.
The evaluation of triple integrals becomes possible because of the three dimensional version of Fubini's theorem. |