Module 6 : PHYSICS OF SEMICONDUCTOR DEVICES
Lecture 34 : p- type Semiconductors
Example 9
  A semiconductor has both p- and n- type impurities. The donor and acceptor levels are 0.1 eV apart. At 300 K, 95% of the acceptor states are found to be occupied. Find the percentage of the donor states which are ionized and determine the position of the Fermi level.
  Solution
  Given
 
$\displaystyle \frac{1}{1+e^{(E_a-E_F})/kT}= 0.05$
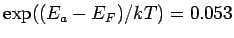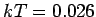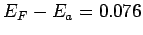  we get $ \exp((E_a-E_F)/kT)= 0.053$. Using $ kT=0.026$ eV corresponding to room temperature, we get $ E_F-E_a= 0.076$ eV. Rewriting this as
 
$\displaystyle E_F-E_d + (E_d-E_a)= E_F-E_d + 0.1 = 0.076$
  which gives 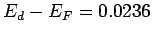$ E_d-E_F= 0.0236$. The occupation probability of the donor level is
 
$\displaystyle \frac{1}{1+e^{(E_d-E_F})/kT}= 0.29$
  Thus 71% of donor atoms are ionized. The Fermi level is situated 0.0236 eV below the donor level.
 

 Back