 |
Example 11 |
| |
Silicon crystal is doped with 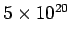 atoms per m atoms per m 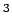 . The donor level is 0.05 eV from the edge of the conduction band. Taking the band gap to be 1.12 eV, calculate the position of the Fermi level at 200 K. . The donor level is 0.05 eV from the edge of the conduction band. Taking the band gap to be 1.12 eV, calculate the position of the Fermi level at 200 K. |
| |
Solution |
| |
The intrinsic carrier concentration can be obtained from the known carrier concentration in Si at 300 K. As the carrier concentration at 300 K is 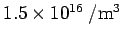 , the carrier concentration at 200 K is , the carrier concentration at 200 K is 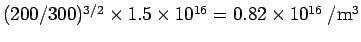 . As the doping concentration is much larger than . As the doping concentration is much larger than 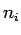 , we can take , we can take 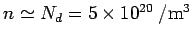 . Thus . Thus |
| |
|
| |
|
|
|