 |
Example 10 |
| |
Pure germanium has a band gap of 0.67 eV. It is doped with 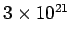 per m per m 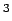 of donor atoms. Find the densities of electrons and holes at 300 K. (effective masses of donor atoms. Find the densities of electrons and holes at 300 K. (effective masses 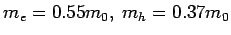 ) ) |
| |
Solution |
| |
For Ge, the intrinsic concentration is |
| |
|
| |
Substituting given numerical values, 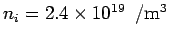 . The density of donor atoms is . The density of donor atoms is 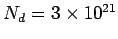 /m /m  . Thus the electron density . Thus the electron density 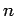 is given by is given by |
| |
|
| |
Thus 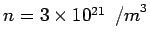 . Using . Using 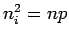 , we get, for the density of holes , we get, for the density of holes 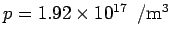 . . |
| |
|
|
|