 |
For a free electron moving under the action of an external force 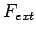 the equation of motion is given by the equation of motion is given by |
| |
Identifying 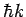 as the momentum of the particle, we have as the momentum of the particle, we have |
| |
We may, therefore, express the mass of the particle in terms of the second derivative of the energy with respect to the wavenumber 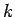 |
| |
The velocity of the particle can be expressed as |