| |
The earth receives 1.4 kW of power from the sun. Assume that both earth and the sun to be black bodies. If the radius of the sun is 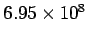 m and the earth-sun distance is m and the earth-sun distance is 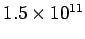 m, calculate the temperature of the sun. m, calculate the temperature of the sun. |
| |
According to Stefan's law, the power radiated by the Sun per unit area is 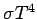 . If 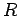 is the radius of the sun, the total power radiated is 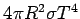 .
|
| |
This power radiates outward from the sun. If at a distance 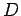 , the power received per unit area is 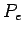 , the total power is equal to the surface area of a sphere of radius 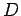 times this amount. Thus, |
| |
Substituting 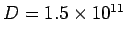 and 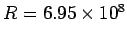 m, we get 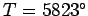 K. |