| |
Estimate the fraction of radiant power of Example 1 which is emitted in the visible region of the spectrum. |
| |
According to Planck's radiation formula, the power per unit area is given by |
| |
Substituting 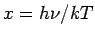 , the expression reduces to , the expression reduces to |
| |
where 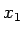 and and 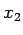 are respectively the upper and the lower limits of are respectively the upper and the lower limits of 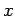 corresponding to visible spectrum. Taking corresponding to visible spectrum. Taking 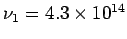 Hz and Hz and 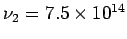 Hz, we get Hz, we get 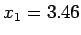 and and 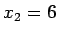 . Thus . Thus |
| |
The integral above has to be done numerically, for instance, by Simpson's method. A crude estimate gives the value of the integral to be approximately 2.41. Thus 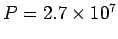 watts, which is about 36% of the total emitted radiation. |