| |
Obtain an expression for the self inductance in a toroid of inner radius 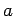 , outer radius , outer radius 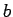 and height and height 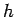 . . |
| |
We have seen that the field inside the toroid at a distance 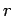 from the axis of the toroid is given by from the axis of the toroid is given by 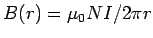 . . |
| |
The flux through one turn of the coil is the integral of this field over the cross section of the coil |
| |
The flux threading 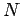 turns is turns is |