 |
A circular loop of radius 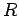 carrying a current carrying a current 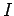 is in the x-y plane. The loop is pivoted about its diameter along the y-axis. A uniform magnetic field is in the x-y plane. The loop is pivoted about its diameter along the y-axis. A uniform magnetic field 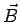 acts parallel to the x-axis. Calculate the torque on the loop. acts parallel to the x-axis. Calculate the torque on the loop.
Solution :
Consider a length element 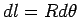 at an angle at an angle 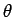 to the y-axis. The force on the element is to the y-axis. The force on the element is 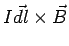 is into the plane of the figure. is into the plane of the figure.
The force on the element is
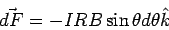
The torque due to this force about the y-axis is
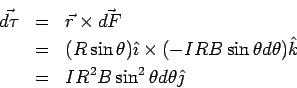
|
|