 |
The length element 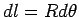 . Since the current direction opposite to the direction of the tangential unit vector . Since the current direction opposite to the direction of the tangential unit vector 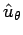 , the vector , the vector 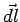 is is
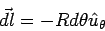
Thus the force is
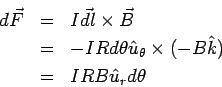
The force on the semicircular arc is obtained by integrating the above. By symmetry, the force on a current element situated at a point Q on the second quadrant, situated symmetrically with P, has the same magnitude and is directed along the radial direction at Q. On resolving the forces along the x and y directions, the components parallel to the x-axis cancel for such symmetric pairs while the component parallel to the y- axis add up. Thus
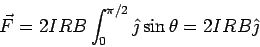
The magnitude of the force is seen to be equal to the product of 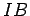 with the diameter of the semi-circle. with the diameter of the semi-circle. |