 |
Consider the dipole shown above, where the charges are separated by a distance 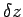 , so that the dipole moment is , so that the dipole moment is 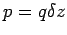 . Let the field at the charge . Let the field at the charge 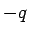 be be 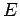 and that at be and that at be 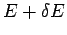 . The force on the charge . The force on the charge 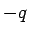 is is 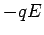 and on and on 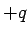 is is 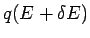 . There is a net force . There is a net force 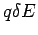 to the right (z-direction). We can write the force as to the right (z-direction). We can write the force as |
| |
where the last equality is valid for an ideal dipole for which 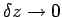 . .
In our case 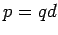 and and |
| |
so that the net force is 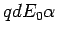 . . |