| |
An intutive form for 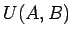 is is
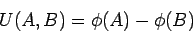
where 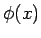 is a scalar function which depends only on the position is a scalar function which depends only on the position 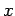 . . 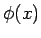 is called the electrostatic potential of the position is called the electrostatic potential of the position 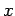 . . 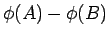 is the potential difference between the positions is the potential difference between the positions 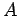 and and 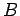 . The absolute value of the potential at a position is meaningless unless we define a reference position at which the potential is zero. Since Coulomb force vanishes only at infinite distances from a source, it is convenient to take infinity to be such a reference position. Thus, the potential at a position . The absolute value of the potential at a position is meaningless unless we define a reference position at which the potential is zero. Since Coulomb force vanishes only at infinite distances from a source, it is convenient to take infinity to be such a reference position. Thus, the potential at a position 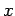 is is
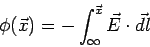
It may be noted that such a reference point is an inappropriate choice for some infinite distribution of charges (e.g. a line charge) where the field does not fall off fast enough to make the integral above vanish. |