| |
Consider a collection of charges 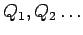 . The electric field at a point due to the distrbution of charges obeys superposition principle. If . The electric field at a point due to the distrbution of charges obeys superposition principle. If 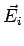 is the electric field at a point P due to the charge is the electric field at a point P due to the charge 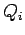 , the net electric field at P is , the net electric field at P is |
| |
The potential 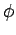 at the point P (with respect to the reference point P at the point P (with respect to the reference point P 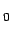 ) is ) is |
| |
where 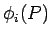 is the potential at P due to the charge is the potential at P due to the charge 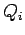 . . |
| |
Determining Electric Field from a knowledge of Potential |
| |
The potential at the position 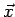 is given by the expression is given by the expression |