| |
Consider a circular strip of radius 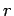 at a depth at a depth 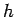 from the apex of the cone. The angle between the electric field through the strip and the vector from the apex of the cone. The angle between the electric field through the strip and the vector 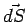 is is 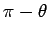 , where , where 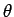 is the semi-angle of the cone. If is the semi-angle of the cone. If 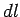 is the length element along the slope, the area of the strip is is the length element along the slope, the area of the strip is 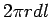 . Thus, . Thus,
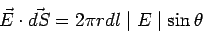
We have, 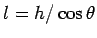 , so that , so that 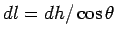 . Further, r = h tan . Further, r = h tan 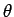 Substituting, we get Substituting, we get
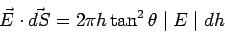
Integrating from 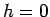 to to 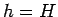 , the height of the cone, the outward flux is , the height of the cone, the outward flux is 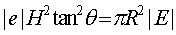 . . |