 |
A vector field is given by 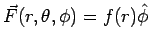 where where 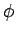 is the azimuthal angle variable of a spherical coordinate system. Calculate the line integral over a circle of radius is the azimuthal angle variable of a spherical coordinate system. Calculate the line integral over a circle of radius 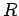 in the x-y plane centered at the origin. Consider an open surface in the form of a hemispherical bowl in the northern hemisphere bounded by the circle. in the x-y plane centered at the origin. Consider an open surface in the form of a hemispherical bowl in the northern hemisphere bounded by the circle. |
| |
On the equatorial circle 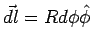 . Hence, . Hence, |
| |
The expression for curl in spherical coordinates may be used to calculate the curl of  . Since the field only has azimuthal component, the curl has radial and polar ( . Since the field only has azimuthal component, the curl has radial and polar (  ) components. ) components. |