 |
A vector field is given by 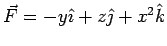 . Calculate the line integral of the field along a circular path of radius . Calculate the line integral of the field along a circular path of radius 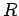 in the x-y plane with its centre at the origin. Verify Stoke's theorem by considering the circle to define (i) the plane of the circle and (ii) a cylinder of height in the x-y plane with its centre at the origin. Verify Stoke's theorem by considering the circle to define (i) the plane of the circle and (ii) a cylinder of height 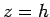 . . |
| |
The curl of 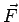 may be calculated as may be calculated as |
| |
Because of symmetry, we use cylindrical (polar) coordinates. The transformations are 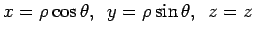 . The unit vectors are . The unit vectors are |