(ii) |
For the cylindrical cup, we have two surfaces : the curved face of the cylinder on which 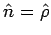 and the top and the top |
 |
circular face on which 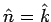 . The contribution from the top circular cap is . The contribution from the top circular cap is 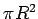 , as before because the two caps only differ in their , as before because the two caps only differ in their 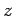 values (the z-component of the curl is independent of values (the z-component of the curl is independent of 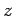 ). The surface integral from the curved surface is (the area element is ). The surface integral from the curved surface is (the area element is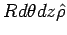 ) ) |
| |
For both the terms of the above integral, the angle integration gives zero. Thus the net surface integral is 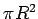 , as expected. , as expected. |