 |
Example 19 :
A vector field is given by 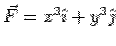 . Verify Divergence theorem for a cylinder of radius 2 and height 5. The origin of the coordinate system is at the centre of the base of the cylinderand z-axis along the axis. . Verify Divergence theorem for a cylinder of radius 2 and height 5. The origin of the coordinate system is at the centre of the base of the cylinderand z-axis along the axis.
Solution :
The problem is obviously simple in cylindrical coordinates. The divergence can be easily seen to be 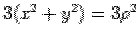 . Recalling that the volume element is . Recalling that the volume element is 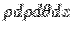 , the integral is , the integral is
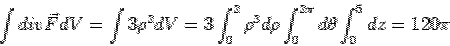
In order to calculate the surface integral, we first observe that the end faces have their normals along 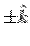 . Since the field does not have any z- component, the contribution to surface integral from the end faces is zero. . Since the field does not have any z- component, the contribution to surface integral from the end faces is zero.
We will calculate the contribution to the surface integral from the curved surface.
|