 |
Find the volume of a solid region in the first octant that is bounded from above by the sphere 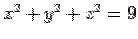 and from below by the cone and from below by the cone 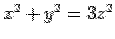 . . |
| |
Because of obvious spherical symmetry, the problem is best solved in spherical polar coordinates. The equation to sphere is 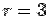 so that the range of so that the range of 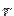 vaiable for our solid is from vaiable for our solid is from 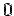 to to 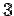 . . |
| |
The equation to the cone 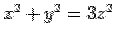 becomes becomes 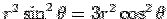 . Solving, the semi-angle of cone is . Solving, the semi-angle of cone is 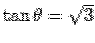 i.e. i.e. 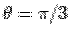 . Since the solid is restricted to the first octant, i.e., ( . Since the solid is restricted to the first octant, i.e., ( 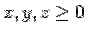 ), the range of the azimuthal angle ), the range of the azimuthal angle 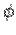 is from is from 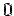 to to 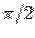 . . |