| |
Find the integral 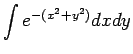 where the region of integration is a unit circle about the origin. where the region of integration is a unit circle about the origin. |
| |
Using polar coordinates the integrand becomes 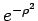 . The range of i integration for . The range of i integration for 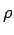 is from is from 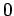 to to 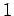 and for and for 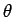 is from is from 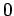 to to 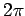 . The integral is given by . The integral is given by |
| |
The radial integral is evaluated by substitution 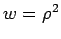 so that so that 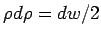 . The value of the integral is . The value of the integral is |