| |
Example 4 :
Find the area of a circle of radius 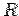 . .
Solution :
Take the origin to be at the centre of the circle and the plane of the circle to be the 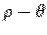 plane. Since the area element in the polar coordinates is plane. Since the area element in the polar coordinates is 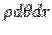 , the area of the circle is , the area of the circle is
![\begin{displaymath}\int_0^{2\pi}d\theta\int_0^R\rho d\rho = 2\pi\left[\frac{\rho^2}{2}\right]_0^R= \pi R^2\end{displaymath}](../../../Text_Template_clip_image127_0002.gif)
a very well known result ! |