| |
Express an arbitray vector 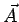 as a linear combination of three non-coplanar vectors as a linear combination of three non-coplanar vectors 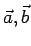 and and 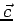 . . |
| |
Let 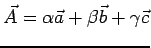 . Since the cross product . Since the cross product 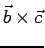 is perpendicular to both is perpendicular to both 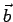 and and 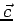 , its dot product with both vectors is zero. Taking the dot product of , its dot product with both vectors is zero. Taking the dot product of 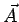 with with 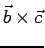 , we have , we have |
| |
The coefficients 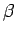 and and 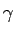 may be found in a similar fashion. may be found in a similar fashion. |