Carrier Density
Density of states
Between the energies E 1 and E 2 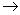 no. of allowed states available to electron/holes in the cited energy range per unit volume of the crystal. no. of allowed states available to electron/holes in the cited energy range per unit volume of the crystal.
From Band theory  difficult difficult
A good approximation can be made from band edges, the regions of bands normally populated by carriers.
For electrons near the bottom of C Band the band forms a pseudo-potential well. The bottom lies at E c and termination of the band at the crystal surface forms the walls of the well. The energy of electrons is relatively small compared with surface barriers. One can think being in a 3 Dimensional box. The density of states at the band edges 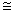 density of states available to a particle of mass m* in a box with dimensions of the potential box density of states available to a particle of mass m* in a box with dimensions of the potential box
Schrödinger equation
Consider a particle of mass a m and total energy E. Size of box 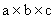
U(x, y, z) = Constant everywhere = 0
Time independent Schrödinger equation,
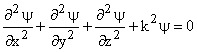 (1) (1)
|
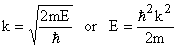 (2) (2)
|
Solve using separation of variables 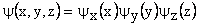
Put in equation 1.
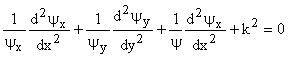 (3) (3)
|
Since k is a constant 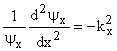
such that
Thus
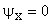 for x = 0, x = a for x = 0, x = a
|
Thus
Similarly
(no. of modes in a 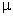 wave resonator) wave resonator)
Thus
Such that
where 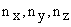 area integers. area integers.
Thus a few discrete energy values are allowed inside.
Allowed solutions/energy/levels
If abc is large, small increments in to 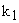 to to 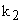 . .
large no. of states allowed  k space and draw. k space and draw.
Fig.6.2
k space vector
end points of all such vectors be dots.
k space unit cell of volume = 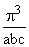 contains one allowed solution. contains one allowed solution.
Thus 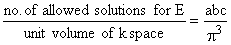 This is not complete. This is not complete.
Now for 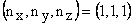
= (-1, 1, 1). . . . . six other possible states for which E is same.
If one counts all points on the k space it is thus necessary to divide by eight to obtain the number of independent solutions.
Thus
But electrons have 2 spin states
Thus
Now number of states with k value between arbitrary k and
k+dk = 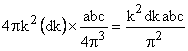 |
Now
Going from k to E space
No. of electron energy states with energy between E and
E+dE = 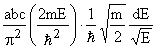 |
Density of energy states with energy between E and E+dE
Now for actual CB or VB densities of state near band edges m 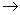 effective mass effective mass 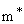
If E c = min CB energy and 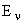 = max VB energy = max VB energy  Bias Bias
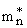 = average effective mass ( = average effective mass ( 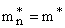 for GaAs or compound semiconductors) for Si or Ge m is complicated. for GaAs or compound semiconductors) for Si or Ge m is complicated.
|