Lattice Vibrations
Consider the ID lattice Fig.5.1
Hooke's law is obeyed exactly
If one atom is displaced by x from equilibrium position
Potential energy of the atom is a function of distance from neighboring atoms Displaced position potential energy is changed by
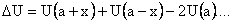 (1) (1)
|
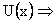 potential energy when distance from neighbour =x potential energy when distance from neighbour =x
Expanding 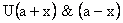 in Taylor series about a and keying only 1st significant term in Taylor series about a and keying only 1st significant term
potential function of a harmonic oscillator
But this
assumption that only one atom oscillates since atoms are bond to each other we expect that vibration of one atom in lattice will set other atom to vibration
let 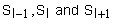 displacement of displacement of 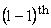 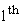 and and 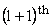 atom from equilibrium atom from equilibrium
Fig.5.2
l = integer
force acting on l th atom, a distance from adjacent atoms and for two adjustment atoms putting it to themselves.
Force F on l th atom
2 nd law to 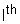 atom atom
.............(i)
Then (i) become
wave equation (ii)
Complex oscillation possible
let regular frequency = 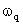 where q = wave no. where q = wave no.
from equation (i).
proper Sign should be chosen to make 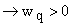
Fig.5.3
Classical single harmonic oscillator there is a single frequency 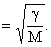
Lattice vibration are characterized by a continum of frequencies with a limiting maximum value 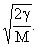 But repetition is there for But repetition is there for 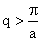 or or 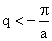
So Brillouin zone concept is coming out.
Now We consider a Crystal of finite member of atoms N
Boundary condition for the displacement of lattice atom at the end of crystal may be taken periodic boundary condition to be no displacement.
Periodic boundary condition
The lattice vibration we talked about applicable to material like  in which all atoms identical and one atom/unit cell. Material with 2 atoms/unit cell or 2 types of atoms/unit cell=Semiconductors. in which all atoms identical and one atom/unit cell. Material with 2 atoms/unit cell or 2 types of atoms/unit cell=Semiconductors.
Double periodicity
Fig.5.4
Two equations describes the vibrations (2 atom 2 period case)
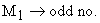
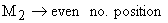
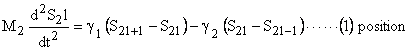
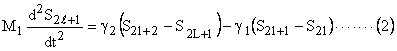
Right hand side is wavelike
|