Concept of Holes
Now consider the 1st band where N states are filled by N electrons at room temperature. With external voltage, electrons will move with velocity  But the band is symmetric about But the band is symmetric about 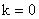 . For every electron with a given . For every electron with a given 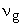 direction, there will be another electron with the same direction, there will be another electron with the same 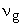 in -x direction. in -x direction.
Thus first band  no current, no current, 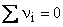
So totally filled energy band do not contribute to the charge transport process.
Thus first band 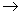 on current, on current, 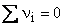
So totally filled energy band do not contribute to the charge transport process.
Asymmetry 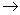 applied electric field. applied electric field.
For nearly empty third band current 
where L 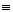 length of 1D crystal and length of 1D crystal and 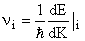
For the nearly filled second band current
This summation is more difficult to evaluate as we have very large number of states filled.
Now if the band was completely filled, 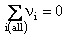
Therefore, we can write
This current is the same as if a positively charge particle is placed on the empty states and the remaining states are unoccupied.
Overall motion of electrons in nearly filled energy band can be described by the empty electronic states provided that the effective mass of the empty states is taken to be negative of 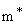 , i.e. , i.e.
Now in this example empty energy states are at the top of the bands 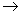 effective mass effective mass 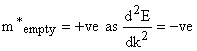 there. Therefore, Empty energy states at the top of a band there. Therefore, Empty energy states at the top of a band 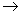 +ve charge with +ve +ve charge with +ve 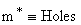
Normally the electron or holes stay mostly at the edge of a band (holes in top of Valence band and electrons in the bottom of conduction band) where parabolic band approximation can be applied. So in semiconductors electrons and holes generally have constant effective mass and the classical treatment/behaviour is a good approximation.
Valence Band
- Maxima occurs at zone center at k = 0
- Valence band =
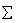 three sub bands three sub bands
Two bands are degenerate (have same allowed energy) at k = 0. Third band max
at reduced energy k =0.
- At k = 0, the shape and curvature are orientation independent.
Conduction Band
- Somewhat similar, but minimum where electrons will gather
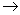 varies from material to material. varies from material to material.
- Ge C Band minima at zone boundary (8 such min)
- Si C Band minima at
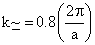 from the zone center. from the zone center.
- GaAs C Band min at k = 0. Direct bandgap good for light emission
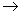 conservation of momentum transition from V Band to C Band. conservation of momentum transition from V Band to C Band.
- 3D structure
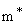 is tensor. is tensor.
Band gap Energy
It is the range from Valence Band maximum to Conduction Band minimum.
At
Si 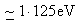 |
GaAs 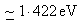 |
A decrease in T results in a contraction of crystal lattice
 stronger atomic bonds stronger atomic bonds
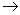 increase in Band gap energy increase in Band gap energy
is a good model
E G 0) |
|
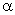
|
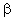
|
Ge |
0.7437 eV |
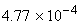
|
235 |
Si |
1.170 eV |
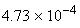
|
636 |
GaAs |
1.519 eV |
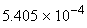
|
204 |
|