From (6.4.7), as k approaches 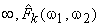 approaches approaches 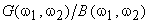 , which is the result of inverse filtering provided that , which is the result of inverse filtering provided that
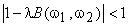 |
(6.4.8) |
To the extent that 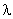 which satisfies (6.4.8) can be found, (6.4.5) can be used in performing inverse filtering. One advantage of the iterative procedure is that it can be stopped after a finite number of iterations. The result after a finite number of iterations is not in general the same as that of inverse filtering, but it is less sensitive to the presence of noise in some cases. which satisfies (6.4.8) can be found, (6.4.5) can be used in performing inverse filtering. One advantage of the iterative procedure is that it can be stopped after a finite number of iterations. The result after a finite number of iterations is not in general the same as that of inverse filtering, but it is less sensitive to the presence of noise in some cases.
Figure 6.12 illustrates the performance of inverse filtering. Figure 6.12(a) shows an original image of 512 x 512 pixels. Figure 6.12(b) shows the original image blurred by a Gaussian-shaped point spread function. The resulting image size is larger than 512 x 512 pixels, but is windowed by a 512 x 512-point rectangular window. The model of the degraded image in the case is
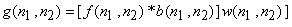 |
(6.4.9) |
Figure 6.12(c) shows the image processed by inverse filtering. The processed image 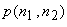 is computed by is computed by
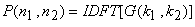 |
(6.4.10) |
where 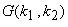 is the DFT of is the DFT of 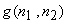 and and 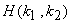 is obtained by is obtained by
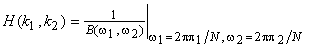 |
(6.4.11) |
The DFT and inverse DFT sizes used are 512 x 512. In the absence of noise and very small 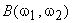 , inverse filtering works quite well despite the fact that , inverse filtering works quite well despite the fact that 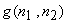 in (6.4.9) is affected by windowing. in (6.4.9) is affected by windowing.
| Figure 6.12 (a) Original image of 512 x 512 pixels |
Figure 6.12 (b)image blurred by a Gaussian-shaped point spread function |
Figure6.12(c) Result of inverse filtering |
|