From (6.2.15) and (6.2.18), the noncausal Wiener filter  is given by is given by
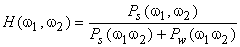 |
(6.2.19) |
Figure 6.1 Application of the noncasual Wiener filter for linear minimum mean square error signal estimation |
Application of the noncausal Wiener filter in (6.2.10) to the signal estimation problem is shown in Figure 6.1. The noncausal Wiener filter has been the basis of many systems developed in such applications as speech enhancement and image restoration. These results can also be applied to solving the linear mean square error estimation problem when 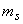 and and 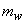 the means of the signal and noise processes, are nonzero. The solution in this case involves subtracting the means of the signal and noise processes, are nonzero. The solution in this case involves subtracting  from the noisy observation from the noisy observation  applying the noncausal Wiener filter developed for zero-mean processes, and adding applying the noncausal Wiener filter developed for zero-mean processes, and adding 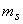 to the resulting signal. This is illustrated in Figure 6.2. to the resulting signal. This is illustrated in Figure 6.2.
Figure 6.2 Linear minimum mean square error estimation of a signal when the signal and noise processes have nonzero means |
If we assume that 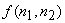 and and 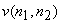 given by equ.(6.2.7), are samples of zero-mean stationary random processes that are linearly independent of each other and that their power spectra given by equ.(6.2.7), are samples of zero-mean stationary random processes that are linearly independent of each other and that their power spectra  and and 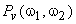 are known, the optimal linear minimum mean square error estimate of are known, the optimal linear minimum mean square error estimate of 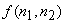 is obtained by filtering is obtained by filtering 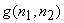 with a Wiener filter whose frequency response with a Wiener filter whose frequency response 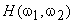 is given by is given by
 |
(6.2.20) |
If we impose the additional constraint that 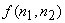 and and 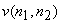 are samples of Gaussian random processes then the Wiener filter in (6.2.20) is the optimal minimum mean square error estimator of the signal among both linear and nonlinear estimators. The Wiener filter was first considered for image restoration in the early 1960s. It has influenced the development of many other image restoration systems. The Wiener filter in (6.2.20) was derived under the assumption that are samples of Gaussian random processes then the Wiener filter in (6.2.20) is the optimal minimum mean square error estimator of the signal among both linear and nonlinear estimators. The Wiener filter was first considered for image restoration in the early 1960s. It has influenced the development of many other image restoration systems. The Wiener filter in (6.2.20) was derived under the assumption that  and and 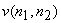 are samples of zero-mean processes. If are samples of zero-mean processes. If  has a mean of has a mean of 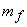 and and 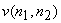 has a mean of has a mean of 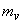 , then , then  and and 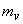 are first subtracted from the degraded are first subtracted from the degraded 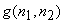 . The resulting signal . The resulting signal 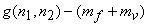 is next filtered by the Wiener filter. The signal mean is next filtered by the Wiener filter. The signal mean  is then added to the filtered signal. This is shown in Figure 6.3. is then added to the filtered signal. This is shown in Figure 6.3.
Figure 6.3 Noncasual Wiener filter for linear minimummean square error estimation of  from from 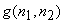 = = + +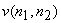 |
The treatment of nonzero means, as shown in Figure 6.3 minimizes the mean square error between 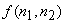 and and 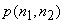 for Gaussian random processes for Gaussian random processes  and and  . It also ensures that . It also ensures that 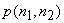 will be an unbiased estimate of will be an unbiased estimate of 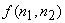 . If . If 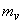 is zero , is zero ,  will be identical to the mean will be identical to the mean 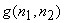 . In this case, . In this case, 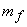 can be estimated from can be estimated from 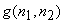 . .
The Wiener filter in (6.2.20) is a zero-phase filter. Since the power spectra 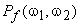 and and 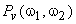 are real and nonnegative, are real and nonnegative,  is also real and nonnegative. Therefore, the Wiener filter preserves the high SNR frequency components while attenuating the low SNR frequency components. If we let is also real and nonnegative. Therefore, the Wiener filter preserves the high SNR frequency components while attenuating the low SNR frequency components. If we let 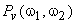 approach approach  will approach 1, indicating that the filter tends to preserve the high SNR frequency components. If we let will approach 1, indicating that the filter tends to preserve the high SNR frequency components. If we let 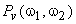 approach approach  will approach 0, indicating that the filter tends to attenuate the low SNR frequency components. will approach 0, indicating that the filter tends to attenuate the low SNR frequency components.
The Wiener filter is based on the assumption that the power spectra  and and  are known or can be estimated. In typical problems, estimating the noise power spectrum are known or can be estimated. In typical problems, estimating the noise power spectrum 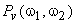 is relatively easy Estimating the image power spectrum is relatively easy Estimating the image power spectrum  is not a simple matter. One method used is to average is not a simple matter. One method used is to average 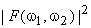 for many different images for many different images 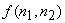 . This is analogous to the periodogram averaging method for spectral estimation. Another method is to model . This is analogous to the periodogram averaging method for spectral estimation. Another method is to model  ,with a simple function such as ,with a simple function such as
 |
(6.2.21a) |
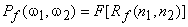 |
(6.2.21b) |
For some constant  . The parameter . The parameter 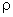 is estimated from the degraded image is estimated from the degraded image 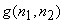 . .
The Wiener filter is generally implemented in the frequency domain by
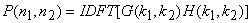 |
(6.2.22) |
The sequences  represent the discrete Fourier transforms (DFTs) of represent the discrete Fourier transforms (DFTs) of 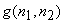 and and 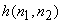 . In (6.2.22), the size of the DFT and inverse DFT is at least (N+M-1) when the image size is N X N and the filter size is M X M, If the DFT size is less that (N+M-1) . In (6.2.22), the size of the DFT and inverse DFT is at least (N+M-1) when the image size is N X N and the filter size is M X M, If the DFT size is less that (N+M-1)  (N+M-1), then the IDFT (N+M-1), then the IDFT  will not be identical to will not be identical to 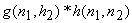 near the boundaries of the processed image near the boundaries of the processed image 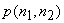 because of aliasing effects. In most cases, however, the effective size of because of aliasing effects. In most cases, however, the effective size of 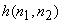 is small, and adequate results can be obtained with a DFT and inverse DFT of size N is small, and adequate results can be obtained with a DFT and inverse DFT of size N  N. One way to obtain N. One way to obtain  is to sample the Wiener filter frequency response is to sample the Wiener filter frequency response 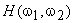 by by
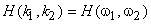 |
evaluated at |
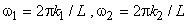 |
(6.2.23) |
where the size of the DFT and inverse DFT is L X L.
The Wiener filter is typically a lowpass filter. Typically, the energy of a typical image is concentrated in low-frequency regions. Since random background noise is generally wideband, the Wiener filter is lowpass in character. This is illustrated in Figure 6.4.
| Figure 6.4 Illustration that the frequency response of a noncasual Wiener filter is typically lowpass in character |
Figure 6.4(a) shows an example of a  which decreases in amplitude as which decreases in amplitude as  and and  increases. Figure 6.4(b) shows an example of a increases. Figure 6.4(b) shows an example of a 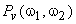 that is constant independent of that is constant independent of 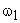 and and 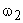 . The resultant Wiener filter . The resultant Wiener filter  given by (6.2.20) is lowpass in character, as shown in figure 6.4(c) given by (6.2.20) is lowpass in character, as shown in figure 6.4(c)
When the information is available, we will use the normalised mean square error (NMSE) between 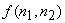 and and 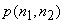 and between and between 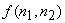 and degraded image and degraded image 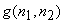 to illustrate the performance of image restoration algorithms. This is defined as to illustrate the performance of image restoration algorithms. This is defined as
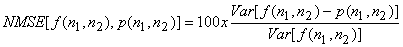 |
(6.2.24) |
where Var[.] is the variance.
|