| Gradient based methods (continued)
Examples of improved estimates of 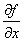 are, are,
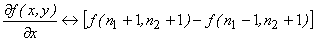  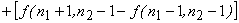
 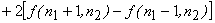
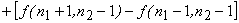
(The scaling factors are neglected)
The differencing operation can be viewed as the convolution of  with impulse response of a filter with impulse response of a filter 
Examples of 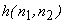 that may be used in directional edge detectors are: that may be used in directional edge detectors are:
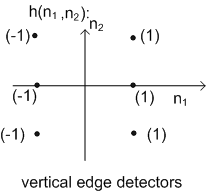
Figure (27a) |
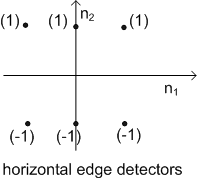
Figure (27b)
|
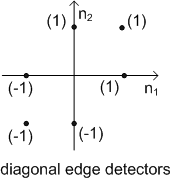
Figure (27c)
|
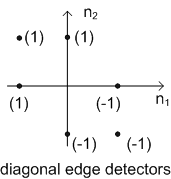
Figure (27d)
|
The 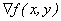 can also be expressed in terms of 1st order partial derivatives in a rotated coordination system. When the rotation is 450 , the direction of partial derivatives are along the two diagonal directions. can also be expressed in terms of 1st order partial derivatives in a rotated coordination system. When the rotation is 450 , the direction of partial derivatives are along the two diagonal directions.
Nondirectional edge detectors can be developed by discrete approx of 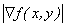 in the edge detector system. in the edge detector system.
As
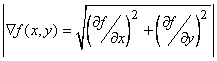 The non directional edge detectors can be developed by nonlinear combination of the terms used in the development of directional edge detectors. Example 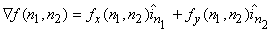
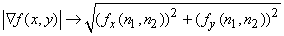
and 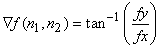
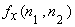 is discrete approximate of is discrete approximate of 
where 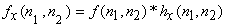
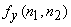 is discrete approximate of is discrete approximate of 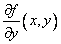
and 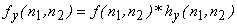
Two filters are necessary because gradient requires the computation of an orthogonal pair of directional derivatives.
where 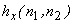 is : is :
Pair of orthogonally oriented filters and
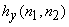 is: is:
And another equation is :
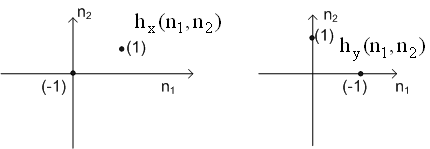
Roberts's edge detector method |
Depending on how 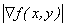 is approximated in the discrete domain, many other variations can be developed. is approximated in the discrete domain, many other variations can be developed.
Roberts operation's components filters are tuned for diagonal edges rather than vertical & horizontal ones. For use in an edge detector based on gradient magnitude, it is important only that the two filters be orthogonal.
|