Differential PCM (continued)
Since prediction of 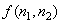 is made in order to reduce the variance of is made in order to reduce the variance of 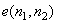 it is reasonable to estimate it is reasonable to estimate 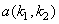 by minimizing, by minimizing,
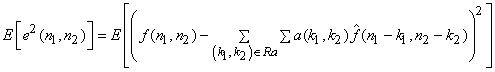 |
(4.8.3) |
Since 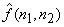 is a function of is a function of 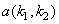 and depends on the specific quantiser used, solving
(4.8.3) is a nonlinear problem. Since and depends on the specific quantiser used, solving
(4.8.3) is a nonlinear problem. Since 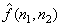 is the quantised version of is the quantised version of 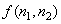 , and is a reasonable representation of , and is a reasonable representation of 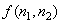 , the prediction coefficients are estimated by minimizing, , the prediction coefficients are estimated by minimizing,
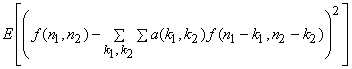 |
(4.8.4) |
Since function minimized is a quadratic form of 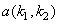 , solving eqn (4.8.4) involves solving a set of linear equations in the form of , solving eqn (4.8.4) involves solving a set of linear equations in the form of
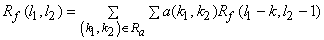 |
(4.8.5) |
where 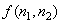 is assumed to be a stationary random process with correlation function is assumed to be a stationary random process with correlation function 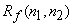 . .
Since a PCM system is a component of a DPCM system, it is possible to use Robert's pseudo noise technique in a DPCM system. However the error signal 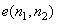 that is quantized in a DPCM type varies rapidly from pixel to pixel and the reconstructed image suffers less from contour problem in a DPCM system than it does in a PCM system. For this reason, Robert's pseudo noise technique that is useful in PCM is not as useful in DPCM system. that is quantized in a DPCM type varies rapidly from pixel to pixel and the reconstructed image suffers less from contour problem in a DPCM system than it does in a PCM system. For this reason, Robert's pseudo noise technique that is useful in PCM is not as useful in DPCM system.
In addition, reducing quantisation noise by using image restoration system is less useful in DPCM system. Both the error sequence 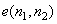 and quantization noise and quantization noise 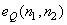 have broad band spectrum and reducing have broad band spectrum and reducing 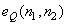 in in 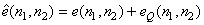 is not very effective. is not very effective.
Since the prediction of 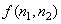 from neighborhood pixels is more difficult in regions such as edges, where local contrast is selectively high, the error signal from neighborhood pixels is more difficult in regions such as edges, where local contrast is selectively high, the error signal 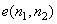 is likely to be large in such regions. A given level of noise is known to be less visible in high contrast than in low contrast regions. This knowledge can be exploited in determining the reconstruction levels of is likely to be large in such regions. A given level of noise is known to be less visible in high contrast than in low contrast regions. This knowledge can be exploited in determining the reconstruction levels of 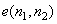 in a DPCM system, since amplitude of in a DPCM system, since amplitude of 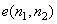 can be related to the amount of local contrast. . can be related to the amount of local contrast. .
|