Properties of optimum Mean square quantizers:
1) The quantizer output is an unbiased estimate of input i.e. 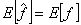
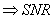 for uniform quantizer increases by 6 dB /bit for uniform quantizer increases by 6 dB /bit
2) The quantizer error is orthogonal to the quantizer output i.e., 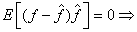 quantization noise is uncorrelated with quantized output. quantization noise is uncorrelated with quantized output.
3) The variance of quantizer 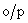 is reduced by the factor is reduced by the factor 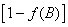 where where 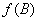 denotes the mean square distortion of the B-bit quantizer for unity variance inputs. denotes the mean square distortion of the B-bit quantizer for unity variance inputs.
i.e. 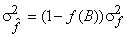
4) It is sufficient to design mean square quantizers for zero mean and unity variance distributions.
Example : Suppose 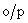 of image sensor takes values from 0 to 10. If samples are quantized uniformly to 256 levels then decision and reconstruction levels are: of image sensor takes values from 0 to 10. If samples are quantized uniformly to 256 levels then decision and reconstruction levels are:
and note 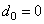 as range is (0,10). as range is (0,10).
and |
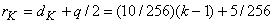 |
Proof of property 1.
1. If 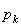 is the probability of is the probability of 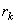 i.e. i.e.
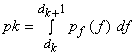
then
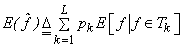
As 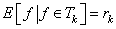 |
we have |
|
Substitute for 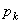 and using the definition of and using the definition of 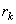 , we have , we have
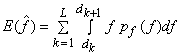
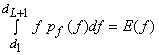
Proof for property 2:
. 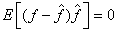 .This implies, .This implies, 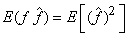
An interesting model for the quantizer follows from this i.e.
is equivalent to
where 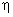 is quantizer noise. is quantizer noise.
As the quantizer noise 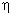 is uncorrelated with is uncorrelated with 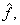 we can write we can write 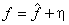
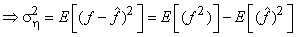
Since  this implies average power of quantizer output is reduced by average power this implies average power of quantizer output is reduced by average power  . .
Also quantizer noise is dependent on input since.
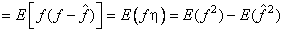
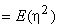
Proof of property 3.
Since for any mean square B-bit quantizer,
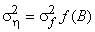
we get from previous results, |
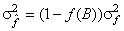 |
|